如图,在⊿ABC中,AB=BC,点D在AB的延长线上。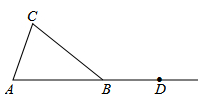
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F.
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由。
相关知识点
推荐套卷
如图,在⊿ABC中,AB=BC,点D在AB的延长线上。
(1)利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法)①作∠CBD的平分线BM ②作边BC上的中线AE,并延长AE交BM于点F.
(2)在(1)的基础上,连接CF,判断四边形ABFC的形状,并说明理由。