如图,在边长为2的等边 中, 是 边上的中点,以点 为圆心, 为半径作圆与 , 分别交于 , 两点,则图中阴影部分的面积为

| A. |
|
B. |
|
C. |
|
D. |
|
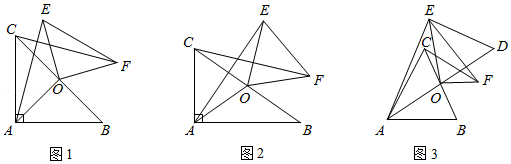
已知在 中, 为 边的中点,连接 ,将 绕点 顺时针方向旋转(旋转角为钝角),得到 ,连接 , .
(1)如图1,当 且 时,则 与 满足的数量关系是 ;
(2)如图2,当 且 时,(1)中的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图3,延长 到点 ,使 ,连接 ,当 , 时,求 的长.
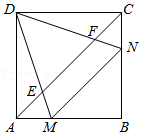
如图,在 中, , , , 为 边上的一个动点,连接 , 为 上的一个动点,连接 , ,当 时,线段 的最小值是

| A. |
3 |
B. |
4 |
C. |
5 |
D. |
6 |
如图,在正方形 中, , 是对角线 上的两点,且 ,连接 并延长交 于点 ,连接 并延长交 于点 ,连接 ,则
| A. |
|
B. |
|
C. |
1 |
D. |
|
如图,在 中, ,作 的垂直平分线交 于点 ,延长 至点 ,使 .
(1)若 ,求 的周长;
(2)若 ,求 的值.

如图,等腰直角三角形 中, , .分别以点 、点 为圆心,线段 长的一半为半径作圆弧,交 、 、 于点 、 、 ,则图中阴影部分的面积为 .

问题解决:如图1,在矩形 中,点 , 分别在 , 边上, , 于点 .
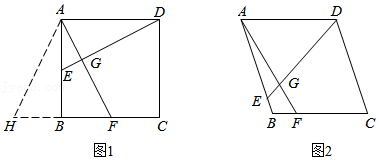
(1)求证:四边形 是正方形;
(2)延长 到点 ,使得 ,判断 的形状,并说明理由.
类比迁移:如图2,在菱形 中,点 , 分别在 , 边上, 与 相交于点 , , , , ,求 的长.
在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知 , 是弦 上一点,请你根据以下步骤完成这个引理的作图过程.
(1)尺规作图(保留作图痕迹,不写作法);
①作线段 的垂直平分线 ,分别交 于点 , 于点 ,连接 , ;
②以点 为圆心, 长为半径作弧,交 于点 , 两点不重合),连接 , , .
(2)直接写出引理的结论:线段 , 的数量关系.

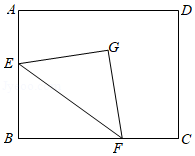
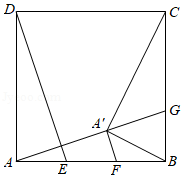
如图,在正方形 中, , 为边 上的两个三等分点,点 关于 的对称点为 , 的延长线交 于点 .
(1)求证: ;
(2)求 的大小;
(3)求证: .
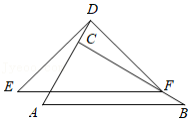
如图,在 中, .线段 是由线段 平移得到的,点 在边 上, 是以 为斜边的等腰直角三角形,且点 恰好在 的延长线上.
(1)求证: ;
(2)求证: .
如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)