如图,在 中, , , ,若以 为直径的 交 于点 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
5 |
将一副直角三角板按如图所示的方式放置,使用 角的三角板的直角边和含 角的三角板的直角边垂直,则 的度数为
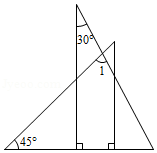
| A. |
|
B. |
|
C. |
|
D. |
|
(1)阅读理解
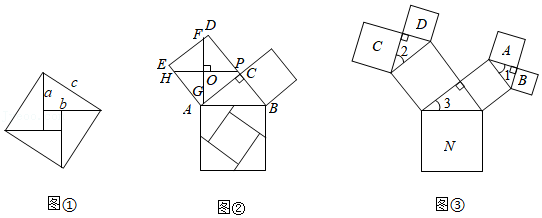
我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.
根据“赵爽弦图”写出勾股定理和推理过程;
(2)问题解决
勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形 的中心 ,作 ,将它分成4份,所分成的四部分和以 为边的正方形恰好能拼成以 为边的正方形.若 , ,求 的值;
(3)拓展探究
如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形 的边长为定值 ,小正方形 , , , 的边长分别为 , , , .
已知 ,当角 变化时,探究 与 的关系式,并写出该关系式及解答过程 与 的关系式用含 的式子表示).
如图,在矩形 中,点 在 上, ,且 ,垂足为 .
(1)求证: ;
(2)若 , ,求四边形 的面积.

在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是 .
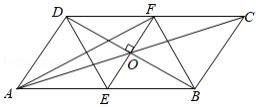
如图,在四边形 中,对角线 与 交于点 ,已知 , ,过点 作 ,分别交 、 于点 , ,连接 , .
(1)求证:四边形 是菱形:
(2)设 , , ,求 的长.
如图, 与等边 的边 , 分别交于点 , , 是直径,过点 作 于点 .
(1)求证: 是 的切线;
(2)连接 ,当 是 的切线时,求 的半径 与等边 的边长 之间的数量关系.

如图,在正六边形 中,连接对角线 , , , , , 与 交于点 , 与 交于点为 , 与 交于点 ,分别延长 , 于点 ,设 .有以下结论:
①
②
③ 的重心、内心及外心均是点
④四边形 绕点 逆时针旋转 与四边形 重合
则所有正确结论的序号是 .

如图, 是等腰三角形, 过原点 ,底边 轴,双曲线 过 , 两点,过点 作 轴交双曲线于点 ,若 ,则 的值是 .

如图,某港口 位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12海里和16海里,1小时后两船分别位于点 , 处,且相距20海里,如果知道甲船沿北偏西 方向航行,则乙船沿 方向航行.

如图,有一池塘,要测池塘两端 、 的距离,可先在平地上取一个点 ,从点 不经过池塘可以直接到达点 和 ,连接 并延长到点 ,使 ,连接 并延长到点 ,使 ,连接 ,那么量出 的长就是 、 的距离,为什么?请结合解题过程,完成本题的证明.
证明:在 和 中,
,
,
.

在 轴, 轴上分别截取 ,再分别以点 , 为圆心,以大于 长为半径画弧,两弧交于点 ,若点 的坐标为 ,则 的值是 .
如图,一次函数 与坐标轴分别交于 , 两点,点 , 分别是线段 , 上的点,且 , ,则点 的标为 .
