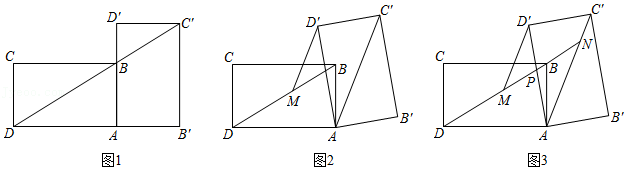
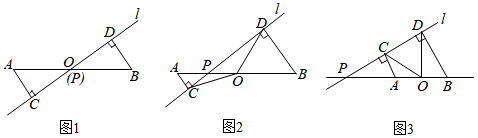
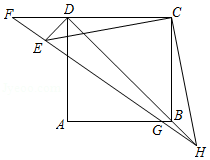
小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形 绕点 顺时针旋转 ,得到矩形 ,连结 .
探究 如图1,当 时,点 恰好在 延长线上.若 ,求 的长.
探究 如图2,连结 ,过点 作 交 于点 .线段 与 相等吗?请说明理由.
探究 在探究2的条件下,射线 分别交 , 于点 , (如图 ,发现线段 , , 存在一定的数量关系,请写出这个关系式,并加以证明.
问题提出
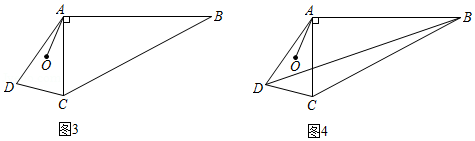
(1)如图1,在 中, , , , 是 的中点,点 在 上,且 ,求四边形 的面积.(结果保留根号)
问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上规划一个五边形河畔公园 .按设计要求,要在五边形河畔公园 内挖一个四边形人工湖 ,使点 、 、 、 分别在边 、 、 、 上,且满足 , .已知五边形 中, , , , , .为满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形 面积的最小值及这时点 到点 的距离;若不存在,请说明理由.
(1)已知 , 如图①摆放,点 , , 在同一条直线上, , .连接 ,过点 作 ,垂足为点 ,直线 交 于点 .求证: .
(2)已知 , 如图②摆放, , .连接 , ,过点 作 ,垂足为点 ,直线 交 于点 .求 的值.
已知点 是线段 的中点,点 是直线 上的任意一点,分别过点 和点 作直线 的垂线,垂足分别为点 和点 .我们定义垂足与中点之间的距离为"足中距".
(1) 猜想验证 如图1,当点 与点 重合时,请你猜想、验证后直接写出"足中距" 和 的数量关系是 .
(2) 探究证明 如图2,当点 是线段 上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由.
(3) 拓展延伸 如图3,①当点 是线段 延长线上的任意一点时,"足中距" 和 的数量关系是否依然成立,若成立,请给出证明;若不成立,请说明理由;
②若 ,请直接写出线段 、 、 之间的数量关系.
课本再现
(1)在证明"三角形内角和定理"时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与 相等的角是 ;

类比迁移
(2)如图2,在四边形 中, 与 互余,小明发现四边形 中这对互余的角可类比(1)中思路进行拼合:先作 ,再过点 作 于点 ,连接 ,发现 , , 之间的数量关系是 ;
方法运用
(3)如图3,在四边形 中,连接 , ,点 是 两边垂直平分线的交点,连接 , .
①求证: ;
②连接 ,如图4,已知 , , ,求 的长(用含 , 的式子表示).
已知四边形 是边长为1的正方形,点 是射线 上的动点,以 为直角边在直线 的上方作等腰直角三角形 , ,设 .
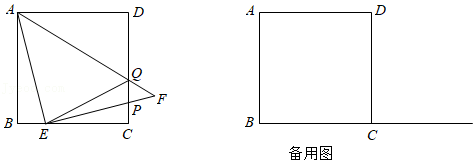
(1)如图,若点 在线段 上运动, 交 于点 , 交 于点 ,连结 ,
①当 时,求线段 的长;
②在 中,设边 上的高为 ,请用含 的代数式表示 ,并求 的最大值;
(2)设过 的中点且垂直于 的直线被等腰直角三角形 截得的线段长为 ,请直接写出 与 的关系式.
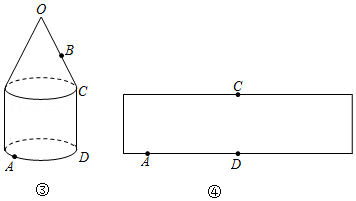
在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为 , 为母线 的中点,点 在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径,并标出它的长(结果保留根号).

(2)图③中的几何体由底面半径相同的圆锥和圆柱组成. 是圆锥的顶点,点 在圆柱的底面圆周上,设圆锥的母线长为 ,圆柱的高为 .
①蚂蚁从点 爬行到点 的最短路径的长为 (用含 , 的代数式表示).
②设 的长为 ,点 在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点 爬行到点 的最短路径的示意图,并写出求最短路径的长的思路.
在数学兴趣小组活动中,小亮进行数学探究活动.
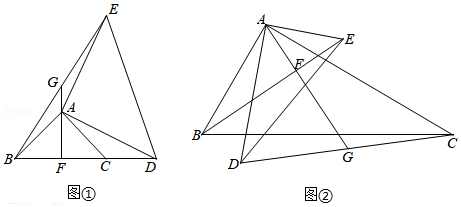
(1) 是边长为3的等边三角形, 是边 上的一点,且 ,小亮以 为边作等边三角形 ,如图1.求 的长;

(2) 是边长为3的等边三角形, 是边 上的一个动点,小亮以 为边作等边三角形 ,如图2.在点 从点 到点 的运动过程中,求点 所经过的路径长;
(3) 是边长为3的等边三角形, 是高 上的一个动点,小亮以 为边作等边三角形 ,如图3.在点 从点 到点 的运动过程中,求点 所经过的路径长;

(4)正方形 的边长为3, 是边 上的一个动点,在点 从点 到点 的运动过程中,小亮以 为顶点作正方形 ,其中点 、 都在直线 上,如图4.当点 到达点 时,点 、 、 与点 重合.则点 所经过的路径长为 ,点 所经过的路径长为 .
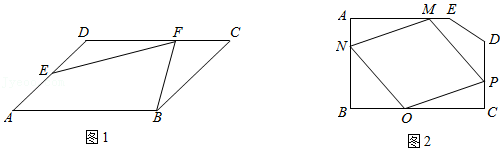
如图1,在 中, , 是 边上的一点, 为 的中点,过点 作 的平行线交 的延长线于 ,且 ,连接 .
(1)求证: ;
(2)在图1中 上取一点 ,使 ,作 关于边 的对称点 ,连接 、 、 、 、 得图2.
①求证: ;
②设 与 相交于点 ,求证: , .

如图所示,四边形 为正方形,在 中, , , 的延长线与 的延长线交于点 ,点 、 、 在同一条直线上.
(1)求证: ;
(2)当 时,求 的值;
(3)当 , 时,求 的值.
下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.
小明:如图1, 分别在射线OA,OB上截取 , 点C,E不重合 ; 分别作线段CE,DF的垂直平分线 , ,交点为P,垂足分别为点G,H; 作射线OP,射线即为 的平分线. 简述理由如下: 由作图知, , , ,所以 ≌ ,则 ,即射线OP是 的平分线. 小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2, 分别在射线OA,OB上截取 , 点C,E不重合 ; 连接DE,CF,交点为P; 作射线 射线OP即为 的平分线.
|
任务:

小明得出 ≌ 的依据是______ 填序号 .
小军作图得到的射线0P是 的平分线吗?请判断并说明理由.
如图3,已知 ,点E,F分别在射线OA,OB上,且 点C,D分别为射线OA,OB上的动点,且 ,连接DE,CF,交点为P,当 时,直接写出线段OC的长.
(1)阅读理解
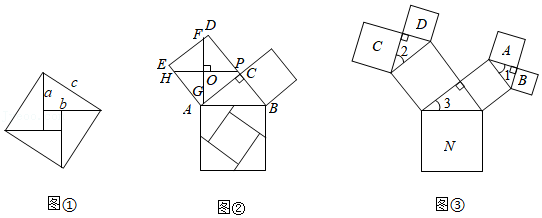
我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.
根据“赵爽弦图”写出勾股定理和推理过程;
(2)问题解决
勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形 的中心 ,作 ,将它分成4份,所分成的四部分和以 为边的正方形恰好能拼成以 为边的正方形.若 , ,求 的值;
(3)拓展探究
如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形 的边长为定值 ,小正方形 , , , 的边长分别为 , , , .
已知 ,当角 变化时,探究 与 的关系式,并写出该关系式及解答过程 与 的关系式用含 的式子表示).