初中数学三角形解答题

已知，为射线上一定点，，为射线上一点，为线段上一动点，连接，满足为钝角，以点为中心，将线段顺时针旋转，得到线段，连接．

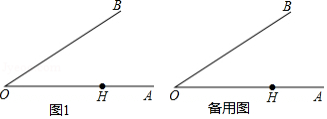
（1）依题意补全图1；

（2）求证：；

（3）点关于点的对称点为，连接．写出一个的值，使得对于任意的点总有，并证明．

如图，在正方形中，是边上的一动点（不与点、重合），连接，点关于直线的对称点为，连接并延长交于点，连接，过点作交的延长线于点，连接．

（1）求证：；

（2）用等式表示线段与的数量关系，并证明．

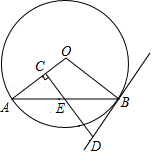
如图，是的直径，过外一点作的两条切线，，切点分别为，，连接，．

（1）求证：；

（2）连接，，若，，，求的长．

如图，在四边形中，，，对角线，交于点，平分，过点作交的延长线于点，连接．

（1）求证：四边形是菱形；

（2）若，，求的长．

下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程．

已知：直线及直线外一点．

求作：直线，使得．

作法：如图，

①在直线上取一点，作射线，以点为圆心，长为半径画弧，交的延长线于点；

②在直线上取一点（不与点重合），作射线，以点为圆心，长为半径画弧，交的延长线于点；

③作直线．所以直线就是所求作的直线．

根据小东设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：　　，　　，

　　（填推理的依据）．

在等腰直角中，，是线段上一动点（与点、不重合），连接，延长至点，使得，过点作于点，交于点．

（1）若，求的大小（用含的式子表示）．

（2）用等式表示线段与之间的数量关系，并证明．

如图，是的一条弦，是的中点，过点作于点，过点作的切线交的延长线于点．

（1）求证：；

（2）若，，求的半径．

如图，在四边形中，为一条对角线，，，，为的中点，连接．

（1）求证：四边形为菱形；

（2）连接，若平分，，求的长．

数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所得两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证．

（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》

请根据该图完成这个推论的证明过程．

证明：，　　　　．

易知，，　　　　，　　　　．

可得．

如图，在中，，，平分交于点．

求证：．

在等边 $\mathit{\Delta ABC}$ 中，

（1）如图1， $P$ ， $Q$ 是 $\mathit{BC}$ 边上的两点， $\mathit{AP}=\mathit{AQ}$ ， $\angle \mathit{BAP}=20°$ ，求 $\angle \mathit{AQB}$ 的度数；

（2）点 $P$ ， $Q$ 是 $\mathit{BC}$ 边上的两个动点（不与点 $B$ ， $C$ 重合），点 $P$ 在点 $Q$ 的左侧，且 $\mathit{AP}=\mathit{AQ}$ ，点 $Q$ 关于直线 $\mathit{AC}$ 的对称点为 $M$ ，连接 $\mathit{AM}$ ， $\mathit{PM}$ ．

①依题意将图2补全；

②小茹通过观察、实验提出猜想：在点 $P$ ， $Q$ 运动的过程中，始终有 $\mathit{PA}=\mathit{PM}$ ，小茹把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

想法1：要证明 $\mathit{PA}=\mathit{PM}$ ，只需证 $\mathit{\Delta APM}$ 是等边三角形；

想法2：在 $\mathit{BA}$ 上取一点 $N$ ，使得 $\mathit{BN}=\mathit{BP}$ ，要证明 $\mathit{PA}=\mathit{PM}$ ，只需证 $\mathit{\Delta ANP}\cong \mathit{\Delta PCM}$ ；

想法3：将线段 $\mathit{BP}$ 绕点 $B$ 顺时针旋转 $60°$ ，得到线段 $\mathit{BK}$ ，要证 $\mathit{PA}=\mathit{PM}$ ，只需证 $\mathit{PA}=\mathit{CK}$ ， $\mathit{PM}=\mathit{CK}\dots$

请你参考上面的想法，帮助小茹证明 $\mathit{PA}=\mathit{PM}$ （一种方法即可）．

如图，在四边形 $\mathit{ABCD}$ 中， $\angle \mathit{ABC}=90°$ ， $\mathit{AC}=\mathit{AD}$ ， $M$ ， $N$ 分别为 $\mathit{AC}$ ， $\mathit{CD}$ 的中点，连接 $\mathit{BM}$ ， $\mathit{MN}$ ， $\mathit{BN}$ ．

（1）求证： $\mathit{BM}=\mathit{MN}$ ；

（2） $\angle \mathit{BAD}=60°$ ， $\mathit{AC}$ 平分 $\angle \mathit{BAD}$ ， $\mathit{AC}=2$ ，求 $\mathit{BN}$ 的长．

如图，四边形 $\mathit{ABCD}$ 是平行四边形， $\mathit{AE}$ 平分 $\angle \mathit{BAD}$ ，交 $\mathit{DC}$ 的延长线于点 $E$ ．求证： $\mathit{DA}=\mathit{DE}$ ．

如图，将正 $n$ 边形绕点 $A$ 顺时针旋转 $60°$ 后，发现旋转前后两图形有另一交点 $O$ ，连接 $\mathit{AO}$ ，我们称 $\mathit{AO}$ 为"叠弦"；再将"叠弦" $\mathit{AO}$ 所在的直线绕点 $A$ 逆时针旋转 $60°$ 后，交旋转前的图形于点 $P$ ，连接 $\mathit{PO}$ ，我们称 $\angle \mathit{OAB}$ 为"叠弦角"， $\mathit{\Delta AOP}$ 为"叠弦三角形"．

[探究证明]

（1）请在图1和图2中选择其中一个证明："叠弦三角形" $\left(\mathit{\Delta AOP}\right)$ 是等边三角形；

（2）如图2，求证： $\angle \mathit{OAB}=\angle \mathit{OAE}\text{'}$ ．

[归纳猜想]

（3）图1、图2中的"叠弦角"的度数分别为 　   ， 　　；

（4）图 $n$ 中，"叠弦三角形" 　　等边三角形（填"是"或"不是" $)$

（5）图 $n$ 中，"叠弦角"的度数为 　　（用含 $n$ 的式子表示）

如图，点 $B$ ， $F$ ， $C$ ， $E$ 在直线 $l$ 上 $(F$ ， $C$ 之间不能直接测量），点 $A$ ， $D$ 在 $l$ 异侧，测得 $\mathit{AB}=\mathit{DE}$ ， $\mathit{AC}=\mathit{DF}$ ， $\mathit{BF}=\mathit{EC}$ ．

（1）求证： $\mathit{\Delta ABC}\cong \mathit{\Delta DEF}$ ；

（2）指出图中所有平行的线段，并说明理由．