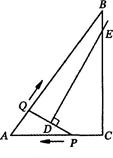
(满分l4分)如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长度的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长度的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB—BC—CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P,Q运动的时间是t s(t>O).
(1)当t=2时,AP=________,点Q到AC的距离是_________;
(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)
(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,请求出t的值;若不能,也请说明理由.