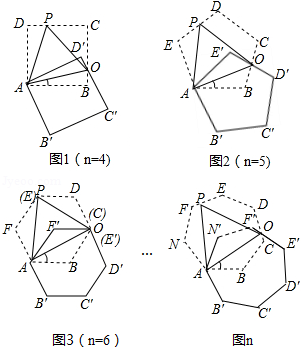
如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)
相关知识点
推荐套卷


 粤公网安备 44130202000953号
粤公网安备 44130202000953号