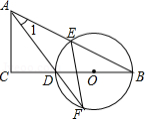
如图, ,点 , 在边 上, , ,点 是边 上的点.若使点 , , 构成等腰三角形的点 恰好有三个,则 的值是 .
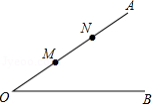
以 的锐角顶点 为圆心,适当长为半径作弧,与边 , 各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点 作直线,与边 交于点 .若 ,点 到 的距离为2,则 的长为 .
如图为某城市部分街道示意图,四边形 为正方形,点 在对角线 上, , , ,小敏行走的路线为 ,小聪行走的路线为 .若小敏行走的路程为 ,则小聪行走的路程为 .

在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图,该图中,四边形 是矩形, 是 延长线上一点, 是 上一点, , .若 ,则 的度数是
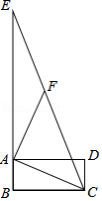
A. B. C. D.
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为
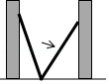
A.0.7米B.1.5米C.2.2米D.2.4米
如图, 是 的中线, 是线段 上一点(不与点 重合). 交 于点 , ,连接 .
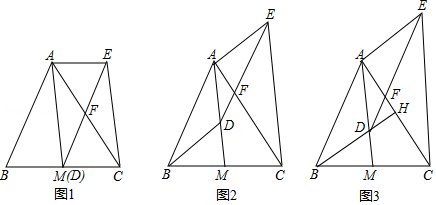
(1)如图1,当点 与 重合时,求证:四边形 是平行四边形;
(2)如图2,当点 不与 重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长 交 于点 ,若 ,且 .
①求 的度数;
②当 , 时,求 的长.
如图,一次函数 与反比例函数 的图象交于点 , .
(1)求这两个函数的表达式;
(2)在 轴上是否存在点 , ,使 为等腰三角形?若存在,求 的值;若不存在,说明理由.

长度分别为2,7, 的三条线段能组成一个三角形, 的值可以是
A.4B.5C.6D.9
已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连接 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.

如图,已知在 中, , , ,点 是 的重心,则点 到 所在直线的距离等于
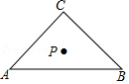
A.1B. C. D.2
如图,在 中, , , 为 边的中点,线段 的垂直平分线交边 于点 .设 , ,则

A. B. C. D.
如图,在 中, , 是 边上一点,以 为直径的 经过 的中点 ,交 的延长线于点 ,连接 .
(1)求证: .
(2)若 , ,求 的长.