初中数学二次函数综合题试题

已知抛物线 $y＝a{x}^2﹣4a（a＞0）$与x轴相交于A，B两点（点A在点B的左侧），点P是抛物线上一点，且 $\mathit{PB}＝\mathit{AB}，$ $\angle \mathit{PBA}＝120°$，如图所示．

（1）求抛物线的解析式．

（2）设点M（m，n）为抛物线上的一个动点，且在曲线PA上移动．

①当点M在曲线PB之间（含端点）移动时，是否存在点M使△APM的面积为 $\frac{5\sqrt{3}}{2}$？若存在，求点M的坐标；若不存在，请说明理由．

②当点M在曲线BA之间（含端点）移动时，求|m|+|n|的最大值及取得最大值时点M的坐标．

如图，抛物线 $y＝a{x}^2+\mathit{bx}+c$（a、b、c为常数， $a\ne 0$）经过点A（﹣1，0），B（5，﹣6），C（6，0）．

（1）求抛物线的解析式；

（2）如图，在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大？若存在，请求出点P的坐标；若不存在，请说明理由；

（3）若点Q为抛物线的对称轴上的一个动点，试指出△QAB为等腰三角形的点Q一共有几个？并请求出其中某一个点Q的坐标．

如图，已知抛物线 $y＝a{x}^2+\mathit{bx}+c（a\ne 0）$经过A（﹣3，0）、B（5，0）、C（0，5）三点，O为坐标原点．

（1）求此抛物线的解析式；

（2）若把抛物线 $y＝a{x}^2+\mathit{bx}+c（a\ne 0）$向下平移 $\frac{\text{13}}{\text{3}}$个单位长度，再向右平移 $n（n＞0）$个单位长度得到新抛物线，若新抛物线的顶点M在△ABC内，求n的取值范围；

（3）设点P在y轴上，且满足 $\angle \mathit{OPA}+\angle \mathit{OCA}＝\angle \mathit{CBA}$，求CP的长．

如图，抛物线y＝ax²+bx+c经过△ABC的三个顶点，与y轴相交于 $(0,\frac{9}{4})$，点A坐标为 $\mathit{（﹣}1,2）$，点B是点A关于y轴的对称点，点C在x轴的正半轴上．

（1）求该抛物线的函数关系表达式．

（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．

（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．

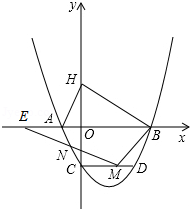
如图，已知抛物线与x轴交于A（﹣1，0），B（4，0），与y轴交于C（0，﹣2）．

（1）求抛物线的解析式；

（2）H是C关于x轴的对称点，P是抛物线上的一点，当△PBH与△AOC相似时，求符合条件的P点的坐标（求出两点即可）；

（3）过点C作 $\mathit{CD}\parallel \mathit{AB}$，CD交抛物线于点D，点M是线段CD上的一动点，作直线MN与线段AC交于点N，与x轴交于点E，且 $\angle \mathit{BME}＝\angle \mathit{BDC}$，当CN的值最大时，求点E的坐标．

如图，抛物线 $y＝a{x}^2+\mathit{bx}-\frac{5}{3}$经过点A（1，0）和点B（5，0），与y轴交于点C．

（1）求抛物线的解析式；

（2）以点A为圆心，作与直线BC相切的⊙A，请判断⊙A与y轴有怎样的位置关系，并说明理由；

（3）在直线BC上方的抛物线上任取一点P，连接PB、PC，请问：△PBC的面积是否存在最大值？若存在，求出这个值和此时点P的坐标；若不存在，请说明理由．

如图，在平面直角坐标系中， O为坐标原点，抛物线 $y＝a{x}^2+2\mathit{xa}+c$ 经过 A（﹣4，0）， B（0，4）两点，与 x轴交于另一点 C，直线 $y＝x+5$ 与 x轴交于点 D，与 y轴交于点 E．

（1）求抛物线的解析式；

（2）点 P是第二象限抛物线上的一个动点，连接 EP，过点 E作 EP的垂线 l，在 l上截取线段 EF，使 EF＝ EP，且点 F在第一象限，过点 F作 $\mathit{FM}\perp x$ 轴于点 M，设点 P的横坐标为 t，线段 FM的长度为 d，求 d与 t之间的函数关系式（不要求写出自变量 t的取值范围）；

（3）在（2）的条件下，过点 E作 $\mathit{EH}\perp \mathit{ED}$ 交 MF的延长线于点 H，连接 DH，点 G为 DH的中点，当直线 PG经过 AC的中点 Q时，求点 F的坐标．

若两条抛物线的顶点相同，则称它们为"友好抛物线"，抛物线 C ₁： y ₁＝﹣2 x ²+4 x+2与 C ₂： y ₂＝﹣ x ²+ mx+ n为"友好抛物线"．

（1）求抛物线 C ₂的解析式．

（2）点 A是抛物线 C ₂上在第一象限的动点，过 A作 AQ⊥ x轴， Q为垂足，求 AQ+ OQ的最大值．

（3）设抛物线 C ₂的顶点为 C，点 B的坐标为（﹣1，4），问在 C ₂的对称轴上是否存在点 M，使线段 MB绕点 M逆时针旋转90°得到线段 MB′，且点 B′恰好落在抛物线 C ₂上？若存在求出点 M的坐标，不存在说明理由．

已知抛物线 $y＝x^2+（2m+1）x+m(m-3)$（m为常数， $﹣1\le m\le 4）$。 $A\mathit{（﹣}m-1，y_1）$， $B\left(\frac{\text{m}}{2},y_2\right)$， $C\mathit{（﹣}m，y_3）$是该抛物线上不同的三点，现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a，过抛物线顶点P作 $\mathit{PH}\perp a$于H．

（1）用含m的代数式表示抛物线的顶点坐标；

（2）若无论m取何值，抛物线与直线 $y＝x-\mathit{km}$（k为常数）有且仅有一个公共点，求k的值；

（3）当 $1＜\mathit{PH}\le 6$时，试比较y₁，y₂，y₃之间的大小．

在平面直角坐标系中，已知抛物线 $y＝x^2+\mathit{bx}+c$的顶点M的坐标为（﹣1，﹣4），且与x轴交于点A，点B（点A在点B的左边），与y轴交于点C．

（1）填空：b＝　　，c＝　　，直线AC的解析式为　　；

（2）直线 $x＝t$与x轴相交于点H．

①当 $t\mathit{＝﹣}3$时得到直线AN（如图1），点D为直线AC下方抛物线上一点，若 $\angle \mathit{COD}＝\angle \mathit{MAN}$，求出此时点D的坐标；

②当 $﹣3＜t\mathit{＜﹣}1$时（如图2），直线 $x＝t$与线段AC，AM和抛物线分别相交于点E，F，P．试证明线段HE，EF，FP总能组成等腰三角形；如果此等腰三角形底角的余弦值为 $\frac{3}{5}$，求此时t的值．

如图，已知点A的坐标为（﹣2，0），直线 $y=-\frac{3}{4}x+3$与x轴、y轴分别交于点B和点C，连接AC，顶点为D的抛物线 $y＝a{x}^2+\mathit{bx}+c$过A、B、C三点．

（1）请直接写出B、C两点的坐标，抛物线的解析式及顶点D的坐标；

（2）设抛物线的对称轴DE交线段BC于点E，P是第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；

（3）设点M是线段BC上的一动点，过点M作 $\mathit{MN}\parallel \mathit{AB}$，交AC于点N，点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒），当t（秒）为何值时，存在△QMN为等腰直角三角形？

如图所示，在平面直角坐标系xOy中，抛物线 $y＝a{x}^2﹣2\mathit{ax}﹣3a（a＜0）$与x轴交于A，B两点（点A在点B的左侧），经过点A的直线 $l：y＝\mathit{kx}+b$与y轴负半轴交于点C，与抛物线的另一个交点为D，且 $\mathit{CD}＝4\mathit{AC}$．

（1）求A、B两点的坐标及抛物线的对称轴；

（2）求直线l的函数表达式（其中k、b用含a的式子表示）；

（3）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为 $\frac{5}{4}$，求a的值；

（4）设P是抛物线对称轴上的一点，点Q在抛物线上，以点A、D、P、Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．

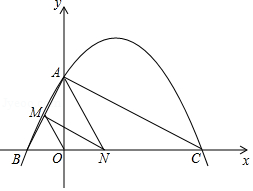
如图，已知二次函数y＝ax²+bx+4的图象与x轴交于点B（﹣2，0），点C（8，0），与y轴交于点A．

（1）求二次函数y＝ax²+bx+4的表达式；

（2）连接AC，AB，若点N在线段BC上运动（不与点B，C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；

（3）连接OM，在（2）的结论下，求OM与AC的数量关系．

如图，抛物线y＝﹣x²+bx+c与直线AB交于A（﹣4，﹣4），B（0，4）两点，直线AC： $y=-\frac{1}{2}x-6$交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．

（1）求抛物线y＝﹣x²+bx+c的表达式；

（2）连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；

（3）①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；

②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求 $\frac{1}{2}$AM+CM它的最小值．

如图1，在平面直角坐标系中，抛物线 y＝ $\frac{\sqrt{3}}{8}$ x ²+ $\frac{3\sqrt{3}}{4}$ x﹣ $\frac{7\sqrt{3}}{8}$ 与 x轴交于点 A、 B（点 A在点 B右侧），点 D为抛物线的顶点，点 C在 y轴的正半轴上， CD交 x轴于点 F，△ CAD绕点 C顺时针旋转得到△ CFE，点 A恰好旋转到点 F，连接 BE．

（1）求点 A、 B、 D的坐标；

（2）求证：四边形 BFCE是平行四边形；

（3）如图2，过顶点 D作 DD ₁⊥ x轴于点 D ₁，点 P是抛物线上一动点，过点 P作 PM⊥ x轴，点 M为垂足，使得△ PAM与△ DD ₁ A相似（不含全等）．

①求出一个满足以上条件的点 P的横坐标；

②直接回答这样的点 P共有几个？