初中数学二次函数综合题试题

如图，抛物线 $y=-\frac{1}{2}{x}^2+\frac{3}{2}x+2$与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

（1）求点A、点B、点C的坐标；

（2）求直线BD的解析式；

（3）当点P在线段OB上运动时，直线l交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；

（4）在点P的运动过程中，是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

如图，在平面直角坐标系xOy中，直线y＝2x+4与y轴交于A点，与x轴交于B点，抛物线 $C_1:y=-\frac{1}{4}{x}^2+\mathit{bx}+c$过A、B两点，与x轴另一交点为C．

（1）求抛物线解析式及C点坐标．

（2）向右平移抛物线C₁，使平移后的抛物线C₂恰好经过△ABC的外心，抛物线C₁、C₂相交于点D，求四边形AOCD的面积．

（3）已知抛物线C₂的顶点为M，设P为抛物线C₁对称轴上一点，Q为抛物线C₁上一点，是否存在以点M、Q、P、B为顶点的四边形为平行四边形？若存在，直接写出P点坐标；不存在，请说明理由．

已知二次函数 y＝ ax ²﹣2 ax+ c（ a＜0）的最大值为4，且抛物线过点（ $\frac{7}{2}$ ，﹣ $\frac{9}{4}$ ，点 P（ t，0）是 x轴上的动点，抛物线与 y轴交点为 C，顶点为 D．

（1）求该二次函数的解析式，及顶点 D的坐标；

（2）求| PC﹣ PD|的最大值及对应的点 P的坐标；

（3）设 Q（0，2 t）是 y轴上的动点，若线段 PQ与函数 y＝ a| x| ²﹣2 a| x|+ c的图象只有一个公共点，求 t的取值．

在平面直角坐标系 xOy中，抛物线 y＝ ax ²+ bx+2过点 A（﹣2，0）， B（2，2），与 y轴交于点 C．

（1）求抛物线 y＝ ax ²+ bx+2的函数表达式；

（2）若点 D在抛物线 y＝ ax ²+ bx+2的对称轴上，求△ ACD的周长的最小值；

（3）在抛物线 y＝ ax ²+ bx+2的对称轴上是否存在点 P，使△ ACP是直角三角形？若存在直接写出点 P的坐标，若不存在，请说明理由．

在平面直角坐标系 xOy中，抛物线 y＝ ax ²+ bx+ c与 y轴交于点 C，其顶点记为 M，自变量 x＝﹣1和 x＝5对应的函数值相等．若点 M在直线 l： y＝﹣12 x+16上，点（3，﹣4）在抛物线上．

（1）求该抛物线的解析式；

（2）设 y＝ ax ²+ bx+ c对称轴右侧 x轴上方的图象上任一点为 P，在 x轴上有一点 A（﹣ $\frac{7}{2}$ ，0），试比较锐角∠ PCO与∠ ACO的大小（不必证明），并写出相应的 P点横坐标 x的取值范围．

（3）直线 l与抛物线另一交点记为 B， Q为线段 BM上一动点（点 Q不与 M重合）．设 Q点坐标为（ t， n），过 Q作 QH⊥ x轴于点 H，将以点 Q， H， O， C为顶点的四边形的面积 S表示为 t的函数，标出自变量 t的取值范围，并求出 S可能取得的最大值．

如图，二次函数 y＝ ax ²+ bx+ c（ a≠0）的图象交 x轴于 A、 B两点，交 y轴于点 D，点 B的坐标为（3，0），顶点 C的坐标为（1，4）．

（1）求二次函数的解析式和直线 BD的解析式；

（2）点 P是直线 BD上的一个动点，过点 P作 x轴的垂线，交抛物线于点 M，当点 P在第一象限时，求线段 PM长度的最大值；

（3）在抛物线上是否存在异于 B、 D的点 Q，使△ BDQ中 BD边上的高为2 $\sqrt{2}$ ？若存在求出点 Q的坐标；若不存在请说明理由．

如图，在平面直角坐标系中，已知抛物线 y＝ $\frac{3}{2}$ x ²+ bx+ c与 x轴交于 A（﹣1，0）， B（2，0）两点，与 y轴交于点 C．

（1）求该抛物线的解析式；

（2）直线 y＝﹣ x+ n与该抛物线在第四象限内交于点 D，与线段 BC交于点 E，与 x轴交于点 F，且 BE＝4 EC．

①求 n的值；

②连接 AC， CD，线段 AC与线段 DF交于点 G，△ AGF与△ CGD是否全等？请说明理由；

（3）直线 y＝ m（ m＞0）与该抛物线的交点为 M， N（点 M在点 N的左侧），点 M关于 y轴的对称点为点 M'，点 H的坐标为（1，0）．若四边形 OM' NH的面积为 $\frac{5}{3}$ ．求点 H到 OM'的距离 d的值．

如图所示，已知抛物线 y＝ ax ²+ bx﹣3经过 A（﹣1，0）， B（4，5）两点，过点 B作 BC⊥ x轴，垂足为 C．

（1）求抛物线的解析式；

（2）求tan∠ ABO的值；

（3）点 M是抛物线上的一个点，直线 MN平行于 y轴交直线 AB于 N，如果以 M， N， B， C为顶点的四边形是平行四边形，求出点 M的横坐标．

如图所示，已知抛物线y＝ax²+bx﹣3经过A（﹣1，0），B（4，5）两点，过点B作BC⊥x轴，垂足为C．

（1）求抛物线的解析式；

（2）求tan∠ABO的值；

（3）点M是抛物线上的一个点，直线MN平行于y轴交直线AB于N，如果以M，N，B，C为顶点的四边形是平行四边形，求出点M的横坐标．

如图，抛物线 y＝﹣ x ²+2 x+3与 x轴相交的于 A， B两点（点 A在点 B的左侧），与 y轴相交于点 C，顶点为 D．

（1）直接写出 A， B， C三点的坐标和抛物线的对称轴；

（2）连接 BC，与抛物线的对称轴交于点 E，点 P为线段 BC上的一个动点（ P不与 C， B两点重合），过点 P作 PF∥ DE交抛物线于点 F，设点 P的横坐标为 m．

①用含 m的代数式表示线段 PF的长，并求出当 m为何值时，四边形 PEDF为平行四边形．

②设△ BCF的面积为 S，求 S与 m的函数关系式；当 m为何值时， S有最大值．

已知抛物线 y＝ ax ²+ bx+ c经过 A（﹣1，0）， B（4，0）， C（0，﹣2）三点．

（1）请直接写出抛物线的解析式．

（2）连接 BC，将直线 BC平移，使其经过点 A，且与抛物线交于点 D，求点 D的坐标．

（3）在（2）中的线段 AD上有一动点 E（不与点 A、点 D重合），过点 E作 x轴的垂线与抛物线相交于点 F，当点 E运动到什么位置时，△ AFD的面积最大？求出此时点 E的坐标和△ AFD的最大面积．

如图，在平面直角坐标系内，抛物线 y＝﹣ x ²+ bx+ c与 x轴交于 A， B两点（ A在 B的左侧），与 y轴交于点 C，且 A， B两点的横坐标分别是方程 x ²﹣2 x﹣3＝0的两个实数根．

（1）求抛物线的解析式．

（2）若抛物线的顶点为 M，作点 M关于 x轴的对称点 N，顺次连接 A， M， B， N，在抛物线上存在点 D，使直线 CD将四边形 AMBN分成面积相等的两个四边形，求点 D的坐标．

（3）在抛物线上是否存在点 P，使△ PBC中 BC边上的高为 $\sqrt{2}$ ？若存在，请直接写出满足条件的所有 P点的坐标；若不存在，请说明理由．

在平面直角坐标系中，已知点 A（﹣2，0）， B（2，0）， C（3，5）．

（1）求过点 A， C的直线解析式和过点 A， B， C的抛物线的解析式；

（2）求过点 A， B及抛物线的顶点 D的⊙ P的圆心 P的坐标；

（3）在抛物线上是否存在点 Q，使 AQ与⊙ P相切，若存在请求出 Q点坐标．

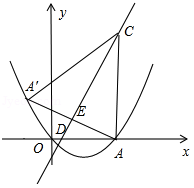
如图所示，抛物线 y＝ ax ²﹣ 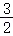x+ c经过原点 O与点 A（6，0）两点，过点 A作 AC⊥ x轴，交直线 y＝2 x﹣2于点 C，且直线 y＝2 x﹣2与 x轴交于点 D．

（1）求抛物线的解析式，并求出点 C和点 D的坐标；

（2）求点 A关于直线 y＝2 x﹣2的对称点 A′的坐标，并判断点 A′是否在抛物线上，并说明理由；

（3）点 P（ x， y）是抛物线上一动点，过点 P作 y轴的平行线，交线段 CA′于点 Q，设线段 PQ的长为 l，求 l与 x的函数关系式及 l的最大值．

如图，二次函数y＝ax²+bx+c的图象交x轴于A、B两点，交y轴于点C，且B（1，0），C（0，3），将△BOC绕点O按逆时针方向旋转90°，C点恰好与A重合．

（1）求该二次函数的解析式；

（2）若点P为线段AB上的任一动点，过点P作PE∥AC，交BC于点E，连结CP，求△PCE面积S的最大值；

（3）设抛物线的顶点为M，Q为它的图象上的任一动点，若△OMQ为以OM为底的等腰三角形，求Q点的坐标．