如图,二次函数 y= ax 2+ bx+ c( a≠0)的图象交 x轴于 A、 B两点,交 y轴于点 D,点 B的坐标为(3,0),顶点 C的坐标为(1,4).
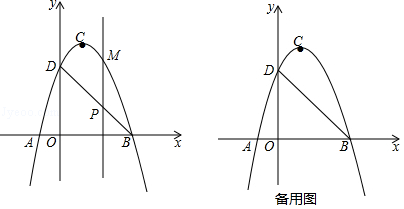
(1)求二次函数的解析式和直线 BD的解析式;
(2)点 P是直线 BD上的一个动点,过点 P作 x轴的垂线,交抛物线于点 M,当点 P在第一象限时,求线段 PM长度的最大值;
(3)在抛物线上是否存在异于 B、 D的点 Q,使△ BDQ中 BD边上的高为2 ?若存在求出点 Q的坐标;若不存在请说明理由.
相关知识点
推荐套卷

 ( )
( ) ( )
( ) (已知)
(已知) (不写作法,保留作图痕迹)求作:∠
(不写作法,保留作图痕迹)求作:∠ ,使得∠
,使得∠ ∠
∠
 中,
中, ,M为AB边上中点,将Rt
,M为AB边上中点,将Rt ,设AE交CB于点N.
,设AE交CB于点N.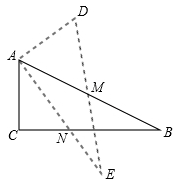
 ,求
,求 的度数;
的度数; 与
与 轴交于A(1,0),
轴交于A(1,0), 两点
两点 
 轴于
轴于 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点 ,使得
,使得 的周长最小?若存在,求出
的周长最小?若存在,求出 个)与它的定价
个)与它的定价 (元/个)的关系如图所示:
(元/个)的关系如图所示:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号