已知抛物线 y＝ ax 2+ bx+ c经过 A（﹣1，0）， B（4，0）， C（0，﹣2）三点．
（1）请直接写出抛物线的解析式．
（2）连接 BC，将直线 BC平移，使其经过点 A，且与抛物线交于点 D，求点 D的坐标．
（3）在（2）中的线段 AD上有一动点 E（不与点 A、点 D重合），过点 E作 x轴的垂线与抛物线相交于点 F，当点 E运动到什么位置时，△ AFD的面积最大？求出此时点 E的坐标和△ AFD的最大面积．
相关试题
某“希望学校”为加强信息技术课教学，拟投资建一个初级计算机房和一个高级计算机房，每个机房只配置1台教师用机，若干台学生用机．现有厂方提供的产品推介单一份，如下表．
产品推介单
| 类别 |
初级机房 |
高级机房 |
| 机型 |
 型 |
 型 |
 型 |
 型 |
|
| 生产 日期 |
2005年1月 |
2005年3月 |
| 单 价 |
型 10000元 |
型 14375元 |
| 型 4375元 |
型 8750元 |
|
| 性能 |
多人交互 |
|
 |
|
|
现知：教师配置
系列机型，学生配置
系列机型；所有机型均按八折优惠销售，两个机房购买计算机的钱数相等，并且每个机房购买计算机的钱数不少于20万元也不超过21万元．
请计算，拟建的两个机房各能配置多少台学生用机？
为美化青岛，创建文明城市，园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配
、
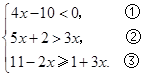
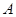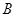两种园艺造型共50个，摆放在迎宾大道两侧．搭配每个造型所需花卉情况如右表所示：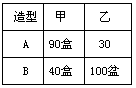
结合上述信息，解答下列问题：
（1）符合题意的搭配方案有哪几种?
（2）若搭配一个种造型的成本为1000元，搭配一个种造型的成本为1200元，试说明选用（1）中哪种方案成本最低？
南宁市是广西最大的罗非鱼养殖产区，被国家农业部列为罗非鱼养殖优势区域．某养殖场计划下半年养殖无公害标准化罗非鱼和草鱼，要求这两个品种总产量
（吨）满足：
，总产值为1000万元．已知相关数据如右表所示．
| 品种 |
单价（万元/吨） |
| 罗非鱼 |
0.45 |
| 草鱼 |
0.85 |
求：该养殖场下半年罗非鱼的产量应控制在什么范围？（产值＝产量
单价）
并将解集在数轴上表示出来.相关知识点
推荐套卷
粤公网安备 44130202000953号