如图,在平面直角坐标系中,点 的坐标是 ,点 为一个动点,过点 作 轴的垂线 ,垂足为 ,点 在运动过程中始终满足 .
【提示:平面直角坐标系内点、的坐标分别为,、,,则】
(1)判断点 在运动过程中是否经过点 ;
(2)设动点 的坐标为 ,求 关于 的函数表达式;填写下表,并在给定坐标系中画出该函数的图象;
|
|
|
0 |
2 |
4 |
6 |
8 |
|
|
|
|
|
|
|
|
|
|
(3)点 关于 轴的对称点为 ,点 在直线 的下方时,求线段 长度的取值范围.

在平面直角坐标系 中,关于 的二次函数 的图象过点 , .
(1)求这个二次函数的表达式;
(2)求当 时, 的最大值与最小值的差;
(3)一次函数 的图象与二次函数 的图象交点的横坐标分别是 和 ,且 ,求 的取值范围.
如图,已知抛物线 过点 .
(1)求抛物线的解析式;
(2)已知直线 过点 , , 且与抛物线交于另一点 ,与 轴交于点 ,求证: ;
(3)若点 , 分别是抛物线与直线 上的动点,以 为一边且顶点为 , , , 的四边形是平行四边形,求所有符合条件的 点坐标.

二次函数 的图象如图所示,下列结论:
① ;② ;③ ;④ .
其中正确结论的个数是

| A. |
4 |
B. |
3 |
C. |
2 |
D. |
1 |
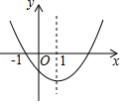
二次函数 的图象如图所示,下列结论:
① ;② ;③ ;④当 时, 随 的增大而减小.
其中正确的有
| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
把抛物线 先向右平移4个单位长度,再向下平移5个单位长度得到抛物线 .
(1)直接写出抛物线 的函数关系式;
(2)动点 能否在抛物线 上?请说明理由;
(3)若点 , 都在抛物线 上,且 ,比较 , 的大小,并说明理由.
抛物线,
,
为常数,
经过
,
两点,下列四个结论:
①一元二次方程的根为
,
;
②若点,
在该抛物线上,则
;
③对于任意实数,总有
;
④对于的每一个确定值,若一元二次方程
为常数,
的根为整数,则
的值只有两个.
其中正确的结论是 (填写序号).
若二次函数 的图象,过不同的六点 、 、 、 , 、 、 ,则 、 、 的大小关系是
| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知二次函数 的图象与 轴相交于 、 两点.则以下结论:① ;②二次函数 的图象的对称轴为 ;③ ;④ .其中正确的有 个.

| A. |
0 |
B. |
1 |
C. |
2 |
D. |
3 |
抛物线 的对称轴直线 .抛物线与 轴的一个交点在点 和点 之间,其部分图象如图所示,下列结论中正确的个数有
① ;② ;③关于 的方程 有两个不相等实数根;④ .
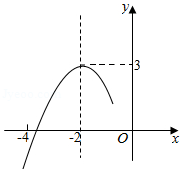
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数(人
与时间
(分钟)的变化情况,数据如下表:(表中
表示
时间 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
人数 |
0 |
170 |
320 |
450 |
560 |
650 |
720 |
770 |
800 |
810 |
810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出与
之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
如图,抛物线与
轴交于
,
两点,与
轴交于点
,抛物线的顶点为
.已知
,
.请答案下列问题:
(1)求抛物线的解析式,并直接写出点的坐标;
(2)抛物线的对称轴与轴交于点
,连接
,
的垂直平分线交直线
于点
,则线段
的长为
.
注:抛物线的对称轴是直线
,顶点坐标是
,
.
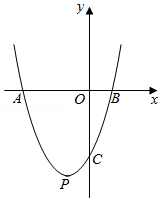
如图,抛物线 与 轴正半轴交于 , 两点,与 轴负半轴交于点 .若点 ,则下列结论中,正确的个数是
① ;
② ;
③ , 与 , 是抛物线上两点,若 ,则 ;
④若抛物线的对称轴是直线 , 为任意实数,则 ;⑤若 ,则 .

| A. |
5 |
B. |
4 |
C. |
3 |
D. |
2 |