初中数学一次函数的应用试题

某公司在甲、乙仓库共存放某种原料450吨，如果运出甲仓库所存原料的 $60\%$，乙仓库所存原料的 $40\%$，那么乙仓库剩余的原料比甲仓库剩余的原料多30吨．

（1）求甲、乙两仓库各存放原料多少吨？

（2）现公司需将300吨原料运往工厂，从甲、乙两个仓库到工厂的运价分别为120元 $/$吨和100元 $/$吨．经协商，从甲仓库到工厂的运价可优惠 $a$元 $/$吨 $(10⩽a⩽30)$，从乙仓库到工厂的运价不变，设从甲仓库运 $m$吨原料到工厂，请求出总运费 $W$关于 $m$的函数解析式（不要求写出 $m$的取值范围）；

（3）在（2）的条件下，请根据函数的性质说明：随着 $m$的增大， $W$的变化情况．

首条贯通丝绸之路经济带的高铁线 $--$宝兰客专进入全线拉通试验阶段．宝兰客专的通车对加快西北地区与“一带一路”沿线国家和地区的经贸合作、人文交流具有十分重要的意义．试运行期间，一列动车从西安开往西宁，一列普通列车从西宁开往西安，两车同时出发，设普通列车行驶的时间为 $x$（小时），两车之间的距离为 $y$（千米），图中的折线表示 $y$与 $x$之间的函数关系，根据图象进行以下探究：

（信息读取）

（1）西宁到西安两地相距　     　千米，两车出发后　    　小时相遇；

（2）普通列车到达终点共需　    　小时，普通列车的速度是　     　千米 $/$小时．

（解决问题）

（3）求动车的速度；

（4）普通列车行驶 $t$小时后，动车到达终点西宁，求此时普通列车还需行驶多少千米到达西安？

草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量 $y$ （千克）与销售单价 $x$ （元）符合一次函数关系，如图是 $y$ 与 $x$ 的函数关系图象．

（1）求 $y$ 与 $x$ 的函数解析式（也称关系式）；

（2）设该水果销售店试销草莓获得的利润为 $W$ 元，求 $W$ 的最大值．

列方程（组）及不等式解应用题

春节期间，某商场计划购进甲、乙两种商品，已知购进甲商品2件和乙商品3件共需270元；购进甲商品3件和乙商品2件共需230元．

（1）求甲、乙两种商品每件的进价分别是多少元？

（2）商场决定甲商品以每件40元出售，乙商品以每件90元出售，为满足市场需求，需购进甲、乙两种商品共100件，且甲种商品的数量不少于乙种商品数量的4倍，请你求出获利最大的进货方案，并确定最大利润．

文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售．甲、乙两种图书的进价分别为每本20元、14元，甲种图书每本的售价是乙种图书每本售价的1.4倍，若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本．

（1）甲乙两种图书的售价分别为每本多少元？

（2）书店为了让利读者，决定甲种图书售价每本降低3元，乙种图书售价每本降低2元，问书店应如何进货才能获得最大利润？（购进的两种图书全部销售完． $)$

“低碳生活，绿色出行”的理念已深入人心，现在越来越多的人选择骑自行车上下班或外出旅游．周末，小红相约到郊外游玩，她从家出发0.5小时后到达甲地，玩一段时间后按原速前往乙地，刚到达乙地，接到妈妈电话，快速返回家中．小红从家出发到返回家中，小红距家的距离 $y\left(\mathit{km}\right)$随时间 $x\left(ℎ\right)$变化的函数图象大致如图所示．

（1）小红从甲地到乙地骑车的速度为　　 $\mathit{km}/ℎ$；

（2）当 $1.5⩽x⩽2.5$时，求出路程 $y\left(\mathit{km}\right)$关于时间 $x\left(ℎ\right)$的函数解析式；并求乙地离小红家多少千米？

甲、乙两人分别从 $A$， $B$两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到达 $B$地后，乙继续前行．设出发 $\mathit{xℎ}$后，两人相距 $\mathit{ykm}$，图中折线表示从两人出发至乙到达 $A$地的过程中 $y$与 $x$之间的函数关系．

根据图中信息，求：

（1）点 $Q$的坐标，并说明它的实际意义；

（2）甲、乙两人的速度．

春季是传染病多发的季节，积极预防传染病是学校高度重视的一项工作，为此，某校对学生宿舍采取喷洒药物的方式进行消毒．在对某宿舍进行消毒的过程中，先经过 $5\mathit{min}$的集中药物喷洒，再封闭宿舍 $10\mathit{min}$，然后打开门窗进行通风，室内每立方米空气中含药量 $y(\mathit{mg}/m^3)$与药物在空气中的持续时间 $x\left(\mathit{min}\right)$之间的函数关系，在打开门窗通风前分别满足两个一次函数，在通风后又成反比例，如图所示．下面四个选项中错误的是 $($　　 $)$

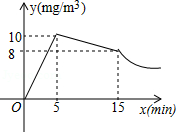
A．经过 $5\mathit{min}$集中喷洒药物，室内空气中的含药量最高达到 $10\mathit{mg}/m^3$

B．室内空气中的含药量不低于 $8\mathit{mg}/m^3$的持续时间达到了 $11\mathit{min}$

C．当室内空气中的含药量不低于 $5\mathit{mg}/m^3$且持续时间不低于35分钟，才能有效杀灭某种传染病毒．此次消毒完全有效             

D．当室内空气中的含药量低于 $2\mathit{mg}/m^3$时，对人体才是安全的，所以从室内空气中的含药量达到 $2\mathit{mg}/m^3$开始，需经过 $59\mathit{min}$后，学生才能进入室内

快递公司为提高快递分拣的速度，决定购买机器人来代替人工分拣．已知购买甲型机器人1台，乙型机器人2台，共需14万元；购买甲型机器人2台，乙型机器人3台，共需24万元．

（1）求甲、乙两种型号的机器人每台的价格各是多少万元；

（2）已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件，该公司计划购买这两种型号的机器人共8台，总费用不超过41万元，并且使这8台机器人每小时分拣快递件数总和不少于8300件，则该公司有哪几种购买方案？哪个方案费用最低，最低费用是多少万元？

$A$、 $B$两地相距 $20\mathit{km}$，甲乙两人沿同一条路线从 $A$地到 $B$地．甲先出发，匀速行驶，甲出发1小时后乙再出发，乙以 $2\mathit{km}/h$的速度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达．甲、乙两人离开 $A$地的距离 $y\left(\mathit{km}\right)$与时间 $t\left(h\right)$的关系如图所示，则甲出发　　小时后和乙相遇．

为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量 $y$（单位：台）和销售单价 $x$（单位：万元）成一次函数关系．

（1）求年销售量 $y$与销售单价 $x$的函数关系式；

（2）根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度 $-{20}^{°}\text{C}$时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到 $-4^{°}\text{C}$时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至 $-{20}^{°}\text{C}$时，制冷再次停止， $\dots$，按照以上方式循环进行．

同学们记录了 $44\mathit{min}$内15个时间点冷柜中的温度 $y{(}^{°}\text{C})$随时间 $x\left(\mathit{min}\right)$的变化情况，制成下表：

时间 $x/\mathit{min}$	$\dots$	4	8	10	16	20	21	22	23	24	28	30	36	40	42	44	$\dots$
温度 $y{/}^{°}\text{C}$	$\dots$	$-20$	$-10$	$-8$	$-5$	$-4$	$-8$	$-12$	$-16$	$-20$	$-10$	$-8$	$-5$	$-4$	$a$	$-20$	$\dots$

（1）通过分析发现，冷柜中的温度 $y$是时间 $x$的函数．

①当 $4⩽x<20$时，写出一个符合表中数据的函数解析式　　；

②当 $20⩽x<24$时，写出一个符合表中数据的函数解析式　　；

（2） $a$的值为　　；

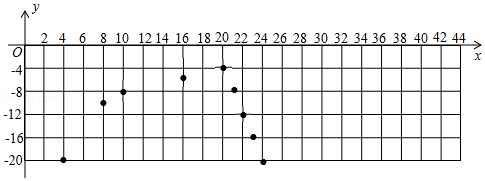
（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当 $4⩽x⩽44$时温度 $y$随时间 $x$变化的函数图象．

某蔬菜加工公司先后两批次收购蒜薹 $($tái $)$共100吨．第一批蒜薹价格为4000元 $/$吨；因蒜薹大量上市，第二批价格跌至1000元 $/$吨．这两批蒜薹共用去16万元．

（1）求两批次购进蒜薹各多少吨？

（2）公司收购后对蒜薹进行加工，分为粗加工和精加工两种：粗加工每吨利润400元，精加工每吨利润1000元．要求精加工数量不多于粗加工数量的三倍．为获得最大利润，精加工数量应为多少吨？最大利润是多少？

$A$， $B$两地相距 $60\mathit{km}$，甲、乙两人从两地出发相向而行，甲先出发．图中 $l_1$， $l_2$表示两人离 $A$地的距离 $s\left(\mathit{km}\right)$与时间 $t\left(h\right)$的关系，请结合图象解答下列问题：

（1）表示乙离 $A$地的距离与时间关系的图象是　　（填 $l_1$或 $l_2)$；甲的速度是　　 $\mathit{km}/h$，乙的速度是　　 $\mathit{km}/h$；

（2）甲出发多少小时两人恰好相距 $5\mathit{km}$？

某市为节约水资源， 制定了新的居民用水收费标准， 按照新标准， 用户每月缴纳的水费 $y$（元 $)$与每月用水量 $x\left(m^3\right)$之间的关系如图所示 ．

（1） 求 $y$关于 $x$的函数解析式；

（2） 若某用户二、 三月份共用水 $40m^3$（二 月份用水量不超过 $25m^3)$，缴纳水费 79.8 元， 则该用户二、 三月份的用水量各是多少 $m^3$？