“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,小红距家的距离 随时间 变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 ;
(2)当 时,求出路程 关于时间 的函数解析式;并求乙地离小红家多少千米?
相关知识点
推荐套卷
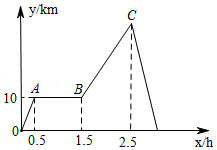
“低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,小红距家的距离 随时间 变化的函数图象大致如图所示.
(1)小红从甲地到乙地骑车的速度为 ;
(2)当 时,求出路程 关于时间 的函数解析式;并求乙地离小红家多少千米?
