初中数学一次函数的应用试题

某长途汽车客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费 $y$（元）是行李质量 $x\left(\mathit{kg}\right)$的一次函数．已知行李质量为 $20\mathit{kg}$时需付行李费2元，行李质量为 $50\mathit{kg}$时需付行李费8元．

（1）当行李的质量 $x$超过规定时，求 $y$与 $x$之间的函数表达式；

（2）求旅客最多可免费携带行李的质量．

张老师计划到超市购买甲种文具100个，他到超市后发现还有乙种文具可供选择．如果调整文具的购买品种，每减少购买1个甲种文具，需增加购买2个乙种文具．设购买 $x$个甲种文具时，需购买 $y$个乙种文具．

（1）①当减少购买1个甲种文具时， $x=$　    　， $y=$　   　；

②求 $y$与 $x$之间的函数表达式．

（2）已知甲种文具每个5元，乙种文具每个3元，张老师购买这两种文具共用去540元．甲、乙两种文具各购买了多少个？

某蓝莓种植生产基地产销两旺，采摘的蓝莓部分加工销售，部分直接销售，且当天都能销售完，直接销售是40元 $/$斤，加工销售是130元 $/$斤（不计损耗）．已知基地雇佣20名工人，每名工人只能参与采摘和加工中的一项工作，每人每天可以采摘70斤或加工35斤．设安排 $x$名工人采摘蓝莓，剩下的工人加工蓝莓．

（1）若基地一天的总销售收入为 $y$元，求 $y$与 $x$的函数关系式；

（2）试求如何分配工人，才能使一天的销售收入最大？并求出最大值．

某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线 $\mathit{ABCD}$表示人均收费 $y$（元）与参加旅游的人数 $x$（人）之间的函数关系．

（1）当参加旅游的人数不超过10人时，人均收费为　    　元；

（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？

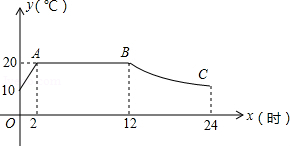
我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为 $15-{20}^{°}\text{C}$的新品种，如图是某天恒温系统从开启到关闭及关闭后，大棚里温度 $y{(}^{°}\text{C})$随时间 $x\left(h\right)$变化的函数图象，其中 $\mathit{AB}$段是恒温阶段， $\mathit{BC}$段是双曲线 $y=\frac{k}{x}$的一部分，请根据图中信息解答下列问题：

（1）求 $k$的值；

（2）恒温系统在一天内保持大棚里温度在 ${15}^{°}\text{C}$及 ${15}^{°}\text{C}$以上的时间有多少小时？

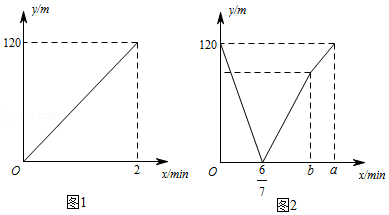
某公司今年如果用原线下销售方式销售一产品，每月的销售额可达100万元．由于该产品供不应求，公司计划于3月份开始全部改为线上销售，这样，预计今年每月的销售额 $y$（万元）与月份 $x$（月）之间的函数关系的图象如图1中的点状图所示（5月及以后每月的销售额都相同），而经销成本 $p$（万元）与销售额 $y$（万元）之间函数关系的图象图2中线段 $\mathit{AB}$所示．

（1）求经销成本 $p$（万元）与销售额 $y$（万元）之间的函数关系式；

（2）分别求该公司3月，4月的利润；

（3）问：把3月作为第一个月开始往后算，最早到第几个月止，该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元？（利润 $=$销售额 $-$经销成本）

如图中的折线 $\mathit{ABC}$表示某汽车的耗油量 $y$（单位： $L/\mathit{km})$与速度 $x$（单位： $\mathit{km}/h)$之间的函数关系 $(30⩽x⩽120)$，已知线段 $\mathit{BC}$表示的函数关系中，该汽车的速度每增加 $1\mathit{km}/h$，耗油量增加 $0.002L/\mathit{km}$．

（1）当速度为 $50\mathit{km}/h$、 $100\mathit{km}/h$时，该汽车的耗油量分别为　 $L/\mathit{km}$、　　 $L/\mathit{km}$．

（2）求线段 $\mathit{AB}$所表示的 $y$与 $x$之间的函数表达式．

（3）速度是多少时，该汽车的耗油量最低？最低是多少？

甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．“五一期间”，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园需购买60元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为 $x$（千克），在甲采摘园所需总费用为 $y_1$（元 $)$，在乙采摘园所需总费用为 $y_2$（元 $)$，图中折线 $\mathit{OAB}$表示 $y_2$与 $x$之间的函数关系．

（1）甲、乙两采摘园优惠前的草莓销售价格是每千克　　元；

（2）求 $y_1$、 $y_2$与 $x$的函数表达式；

（3）在图中画出 $y_1$与 $x$的函数图象，并写出选择甲采摘园所需总费用较少时，草莓采摘量 $x$的范围．

一条公路旁依次有 $A$， $B$， $C$三个村庄，甲乙两人骑自行车分别从 $A$村、 $B$村同时出发前往 $C$村，甲乙之间的距离 $s\left(\mathit{km}\right)$与骑行时间 $t\left(h\right)$之间的函数关系如图所示，下列结论：

① $A$， $B$两村相距 $10\mathit{km}$；

②出发 $1.25h$后两人相遇；

③甲每小时比乙多骑行 $8\mathit{km}$；

④相遇后，乙又骑行了 $15\mathit{min}$或 $65\mathit{min}$时两人相距 $2\mathit{km}$．

其中正确的个数是 $($　　 $)$

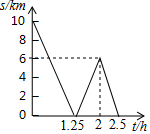
A．1个B．2个C．3个D．4个

甲、乙两人分别从 $A$， $B$两地相向而行，匀速行进甲先出发且先到达 $B$地，他们之间的距离 $s\left(\mathit{km}\right)$与甲出发的时间 $t\left(ℎ\right)$的关系如图所示，则乙由 $B$地到 $A$地用了　10　 $ℎ$．

某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元．销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件．同时，在销售过程中，每月还要支付其他费用450元．设销售单价为 $x$元，平均月销售量为 $y$件．

（1）求出 $y$与 $x$的函数关系式，并写出自变量 $x$的取值范围．

（2）当销售单价为多少元时，销售这种童装每月可获利1800元？

（3）当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？

甲、乙两人沿同一条直路走步，如果两人分别从这条直路上的 $A$， $B$两处同时出发，都以不变的速度相向而行，图1是甲离开 $A$处后行走的路程 $y$（单位： $m)$与行走时间 $x$（单位： $\mathit{min})$的函数图象，图2是甲、乙两人之间的距离 $y$（单位： $m)$与甲行走时间 $x$（单位： $\mathit{min})$的函数图象，则 $a-b=$　　．

随着人们生活水平的提高，短途旅行日趋火爆．我市某旅行社推出“辽阳 $-$葫芦岛海滨观光一日游”项目，团队人均报名费用 $y$（元 $)$与团队报名人数 $x$（人 $)$之间的函数关系如图所示，旅行社规定团队人均报名费用不能低于88元．旅行社收到的团队总报名费用为 $w$（元 $)$．

（1）直接写出当 $x⩾20$时， $y$与 $x$之间的函数关系式及自变量 $x$的取值范围；

（2）儿童节当天旅行社收到某个团队的总报名费为3000元，报名旅游的人数是多少？

（3）当一个团队有多少人报名时，旅行社收到的总报名费最多？最多总报名费是多少元？

晓琳和爸爸到太子河公园运动，两人同时从家出发，沿相同路线前行，途中爸爸有事返回，5分钟后晓琳也原路返回，两人恰好同时到家．晓琳和爸爸在整个运动过程中离家的路程 $y_1$（米 $)$， $y_2$（米 $)$与运动时间 $x$（分 $)$之间的函数关系如图所示，下列结论：①两人同行过程中的速度为200米 $/$分；② $m$的值是15， $n$的值是3000；③晓琳开始返回时与爸爸相距1800米；④运动18分钟或30分钟时，两人相距900米．其中正确结论的个数是 $($　　 $)$

A．1个B．2个C．3个D．4个

甲、乙两人分别从 $A$， $B$两地相向而行，他们距 $B$地的距离 $s\left(\mathit{km}\right)$与时间 $t\left(ℎ\right)$的关系如图所示，那么乙的速度是　　 $\mathit{km}/ℎ$．