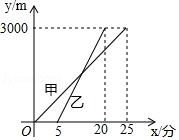
赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点 驶向终点 ,在整个行程中,龙舟离开起点的距离 (米 与时间 (分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点 与终点 之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的 与 函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
某商店以20元 千克的单价新进一批商品,经调查发现,在一段时间内,销售量 (千克)与销售单价 (元 千克)之间为一次函数关系,如图所示.
(1)求 与 的函数表达式;
(2)要使销售利润达到800元,销售单价应定为每千克多少元?

某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修.现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元.学校要求在12天内将学生公寓楼装修完成.若完成该工程甲队工作 天,乙队工作 天.求学校需支付的总工资 (元 与甲队工作天数 (天 的函数关系式,并求出 的取值范围及 的最小值.
某新建成学校举行美化绿化校园活动,九年级计划购买 , 两种花木共100棵绿化操场,其中 花木每棵50元, 花木每棵100元.
(1)若购进 , 两种花木刚好用去8000元,则购买了 , 两种花木各多少棵?
(2)如果购买 花木的数量不少于 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用.
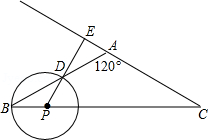
如图, 中, , . 是底边 上的一个动点 与 、 不重合),以 为圆心, 为半径的 与射线 交于点 ,射线 交射线 于点 .
(1)若点 在线段 的延长线上,设 , ,求 关于 的函数关系式,并写出 的取值范围.
(2)当 时,试说明射线 与 是否相切.
(3)连接 ,若 ,求 的长.
我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元,相关资料表明:甲、乙两种鱼苗的成活率为 ,
(1)若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?
(2)若要使这批鱼苗的总成活率不低于 ,则乙种鱼苗至少购买多少条?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?
如图,小明购买一种笔记本所付款金额 (元 与购买量 (本 之间的函数图象由线段 和射线 组成,则一次购买8个笔记本比分8次购买每次购买1个可节省 元.

都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为 .
运行区间 |
票价 |
||
起点站 |
终点站 |
一等座 |
二等座 |
都匀 |
桂林 |
95(元 |
60(元 |
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买 张 参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用 与 之间的函数关系式.
(3)在(2)的方案下,请求出当 时,购买单程火车票的总费用.
为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展.2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元 公顷,青椒1.5万元 公顷,马铃薯2万元 公顷,设种植西红柿 公顷,总利润为 万元.
(1)求总利润 (万元)与种植西红柿的面积 (公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的 在冬季同时建造 、 两种类型的温室大棚,开辟新的经济增长点,经测算,投资 种类型的大棚5万元 个, 种类型的大棚8万元 个,请直接写出有哪几种建造方案?
在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地.两车同时出发,匀速行驶,客车、货车离服务区的距离 (千米), (千米)与行驶的时间 (小时)的函数关系图象如图1所示.
(1)甲、乙两地相距 千米.
(2)求出发3小时后,货车离服务区的路程 (千米)与行驶时间 (小时)之间的函数关系式.
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离 (千米)与行驶时间 (小时)之间的函数关系图线如图2中的虚线所示,直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等?

, , 三地在同一条公路上, 地在 , 两地之间,甲、乙两车同时从 地出发匀速行驶,甲车驶向 地,乙车先驶向 地,到达 地后,调头按原速经过 地驶向 地(调头时间忽略不计),到达 地停止行驶,甲车比乙车晚0.4小时到达 地,两车距 地的路程 与行驶时间 之间的函数关系如图所示,请结合图象信息,解答下列问题:
(1)甲车行驶的速度是 ,并在图中括号内填入正确的数值;
(2)求图象中线段 所表示的 与 的函数解析式(不需要写出自变量 的取值范围);
(3)在乙车到达 地之前,甲、乙两车出发后几小时与 地路程相等?直接写出答案.

下列图象中,能反映等腰三角形顶角 (度 与底角 (度 之间的函数关系的是
A.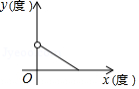 B.
B.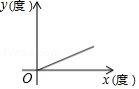
C.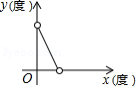 D.
D.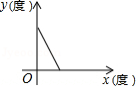
某快递公司的每位“快递小哥”日收入与每日的派送量成一次函数关系,如图所示.
(1)求每位“快递小哥”的日收入 (元 与日派送量 (件 之间的函数关系式;
(2)已知某“快递小哥”的日收入不少于110元,则他至少要派送多少件?

我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进 、 两种型号的电动自行车共30辆,其中每辆 型电动自行车比每辆 型电动自行车多500元.用5万元购进的 型电动自行车与用6万元购进的 型电动自行车数量一样.
(1)求 、 两种型号电动自行车的进货单价;
(2)若 型电动自行车每辆售价为2800元, 型电动自行车每辆售价为3500元,设该商店计划购进 型电动自行车 辆,两种型号的电动自行车全部销售后可获利润 元.写出 与 之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
某校喜迎中华人民共和国成立70周年,将举行以“歌唱祖国”为主题的歌咏比赛,需要在文具店购买国旗图案贴纸和小红旗发给学生做演出道具.已知每袋贴纸有50张,每袋小红旗有20面,贴纸和小红旗需整袋购买,每袋贴纸价格比每袋小红旗价格少5元,用150元购买贴纸所得袋数与用200元购买小红旗所得袋数相同.
(1)求每袋国旗图案贴纸和每袋小红旗的价格各是多少元?
(2)如果给每位演出学生分发国旗图案贴纸2张,小红旗1面.设购买国旗图案贴纸 袋 为正整数),则购买小红旗多少袋能恰好配套?请用含 的代数式表示.
(3)在文具店累计购物超过800元后,超出800元的部分可享受8折优惠.学校按(2)中的配套方案购买,共支付 元,求 关于 的函数关系式.现全校有1200名学生参加演出,需要购买国旗图案贴纸和小红旗各多少袋?所需总费用多少元?