初中数学一次函数的应用试题

明君社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率．该绿化组完成的绿化面积 S（单位： m ²）与工作时间 t（单位： h）之间的函数关系如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（　　）

A．

$300m^2$

B．

$150m^2$

C．

$330m^2$

D．

$450m^2$

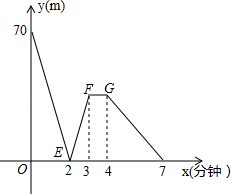
有一科技小组进行了机器人行走性能试验，在试验场地有 A、 B、 C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从 A、 B两点同时同向出发，历时7分钟同时到达 C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离 y（米）与他们的行走时间 x（分钟）之间的函数图象，请结合图象，回答下列问题：

（1） A、 B两点之间的距离是 　　米，甲机器人前2分钟的速度为 　　米/分；

（2）若前3分钟甲机器人的速度不变，求线段 EF所在直线的函数解析式；

（3）若线段 FG∥ x轴，则此段时间，甲机器人的速度为 　　米/分；

（4）求 A、 C两点之间的距离；

（5）若前3分钟甲机器人的速度不变，直接写出两机器人出发多长时间相距28米．

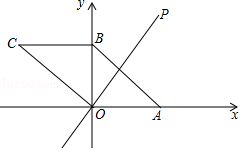
点 P（ x， y）在第一象限内，且 x+ y＝6，点 A的坐标为（4，0）．设△ OPA的面积为 S，则下列图象中，能正确反映面积 S与 x之间的函数关系式的图象是（　　）

A．		B．
C．		D．

由于持续高温和连日无雨，某水库的蓄水量随时间的增加而减少，已知原有蓄水量 y ₁（万 m ³）与干旱持续时间 x（天）的关系如图中线段 l ₁所示，针对这种干旱情况，从第20天开始向水库注水，注水量 y ₂（万 m ³）与时间 x（天）的关系如图中线段 l ₂所示（不考虑其它因素）．

（1）求原有蓄水量 y ₁（万 m ³）与时间 x（天）的函数关系式，并求当 x＝20时的水库总蓄水量．

（2）求当0≤ x≤60时，水库的总蓄水量 y（万 m ³）与时间 x（天）的函数关系式（注明 x的范围），若总蓄水量不多于900万 m ³为严重干旱，直接写出发生严重干旱时 x的范围．

孝感市在创建国家级园林城市中，绿化档次不断提升．某校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

（1）求A种，B种树木每棵各多少元？

（2）因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

如图，在平面直角坐标系xOy中，▱ABCO的顶点A，B的坐标分别是A（3，0），B（0，2）．动点P在直线 $y=\frac{3}{2}x$上运动，以点P为圆心，PB长为半径的⊙P随点P运动，当⊙P与▱ABCO的边相切时，P点的坐标为　　．

有 A、 B两个发电厂，每焚烧一吨垃圾， A发电厂比 B发电厂多发40度电， A焚烧20吨垃圾比 B焚烧30吨垃圾少1800度电．

（1）求焚烧1吨垃圾， A和 B各发电多少度？

（2） A、 B两个发电厂共焚烧90吨的垃圾， A焚烧的垃圾不多于 B焚烧的垃圾两倍，求 A厂和 B厂总发电量的最大值．

某书店在"读书节"之前，图书按标价销售，在"读书节"期间制定了活动计划．

（1）"读书节"之前小明发现：购买5本 A图书和8本 B图书共花279元，购买10本 A图书比购买6本 B图书多花162元，请求出 A、 B图书的标价；

（2）"读书节"期间书店计划用不超过3680元购进 A、 B图书共200本，且 A图书不少于50本， A、 B两种图书进价分别为24元、16元；销售时准备 A图书每本降价1.5元， B图书价格不变，那么书店如何进货才能使利润最大？

某工厂制作 A， B两种手工艺品， B每件获利比 A多105元，获利30元的 A与获利240元的 B数量相等．

（1）制作一件 A和一件 B分别获利多少元？

（2）工厂安排65人制作 A， B两种手工艺品，每人每天制作2件 A或1件 B．现在在不增加工人的情况下，增加制作 C．已知每人每天可制作1件 C（每人每天只能制作一种手工艺品），要求每天制作 A， C两种手工艺品的数量相等．设每天安排 x人制作 B， y人制作 A，写出 y与 x之间的函数关系式．

（3）在（1）（2）的条件下，每天制作 B不少于5件．当每天制作5件时，每件获利不变．若每增加1件，则当天平均每件获利减少2元．已知 C每件获利30元，求每天制作三种手工艺品可获得的总利润 W（元）的最大值及相应 x的值．

如图，已知 A（6，0）， B（8，5），将线段 OA平移至 CB，点 D在 x轴正半轴上（不与点 A重合），连接 OC， AB， CD， BD．

（1）求对角线 AC的长；

（2）设点 D的坐标为（ x，0），△ ODC与△ ABD的面积分别记为 S ₁， S ₂．设 S＝ S ₁﹣ S ₂，写出 S关于 x的函数解析式，并探究是否存在点 D使 S与△ DBC的面积相等？如果存在，用坐标形式写出点 D的位置；如果不存在，说明理由．

如图是本地区一种产品30天的销售图象，图①是产品日销售量 y（单位：件）与时间 t（单位：天）的函数关系，图②是一件产品的销售利润 z（单位：元）与时间 t（单位：天）的函数关系，已知日销售利润＝日销售量×一件产品的销售利润．下列结论错误的是（　　）

A．	第24天的销售量为300件
B．	第10天销售一件产品的利润是15元
C．	第27天的日销售利润是1250元
D．	第15天与第30天的日销售量相等

某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如表：

产品	每件售价（万元）	每件成本（万元）	每年其他费用（万元）	每年最大产销量（件）
甲	6	a	20	200
乙	20	10	40+0.05x^2	80

其中a为常数，且 $3\le a\le 5$。

（1）若产销甲、乙两种产品的年利润分别为y₁万元、y₂万元，直接写出y₁、y₂与x的函数关系式；

（2）分别求出产销两种产品的最大年利润；

（3）为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．

一茶叶专卖店经销某种品牌的茶叶，该茶叶的成本价是80元/kg，销售单价不低于120元/kg．且不高于180元/kg，经销一段时间后得到如下数据：

销售单价x（元/kg）	120	130	…	180
每天销量y（kg）	100	95	…	70

设y与x的关系是我们所学过的某一种函数关系．

（1）直接写出y与x的函数关系式，并指出自变量x的取值范围；

（2）当销售单价为多少时，销售利润最大？最大利润是多少？

为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种树苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．

（1）求y与x的函数关系式；

（2）若在购买计划中，B种树苗的数量不超过35棵，但不少于A种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．

A城有某种农机30台，B城有该农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36台，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．

（1）设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数关系式，并写出自变量x的取值范围；

（2）现该运输公司要求运送全部农机的总费用不低于16460元，则有多少种不同的调运方案？将这些方案设计出来；

（3）现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元（a≤200）作为优惠，其它费用不变，如何调运，使总费用最少？