某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修.现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元.学校要求在12天内将学生公寓楼装修完成.若完成该工程甲队工作 天,乙队工作 天.求学校需支付的总工资 (元 与甲队工作天数 (天 的函数关系式,并求出 的取值范围及 的最小值.
相关知识点
推荐套卷

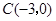 ,点
,点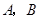 分别在
分别在 轴,
轴,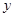 轴的正半轴上,且满足
轴的正半轴上,且满足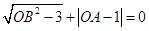 .
.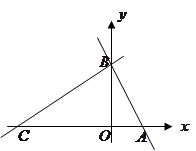
 ,点
,点 的坐标
的坐标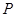 从
从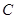 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段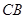 运动,连结
运动,连结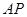 .设
.设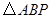 的面积为
的面积为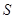 ,点
,点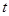 秒,求
秒,求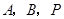 为顶点的三角形与
为顶点的三角形与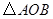 相似?若存在,请直接写出点
相似?若存在,请直接写出点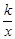 (k>0)与直线y=k'x交于A、B两点,点A在第一象限.
(k>0)与直线y=k'x交于A、B两点,点A在第一象限.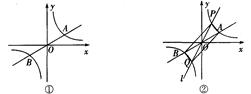

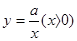 的图象与直线
的图象与直线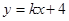 相交于点A(1,3)、B(
相交于点A(1,3)、B(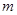 ,1)两点,
,1)两点,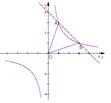
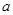 、
、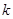 、
、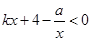 的解(请直接写出答案);
的解(请直接写出答案); 粤公网安备 44130202000953号
粤公网安备 44130202000953号