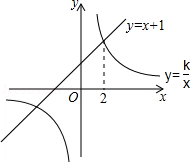如图,一次函数 与反比例函数 的图象交于
点 和 ,与 轴交于点 .
(1)求一次函数和反比例函数的解析式;
(2)在 轴上取一点 ,当 的面积为3时,求点 的坐标;
(3)将直线 向下平移2个单位后得到直线 ,当函数值 时,求 的取值范围.
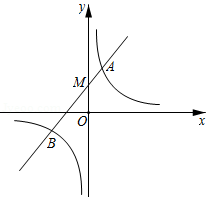
一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)求一次函数的解析式;
(2)将直线 沿 轴向下平移8个单位后得到直线 , 与两坐标轴分别相交于 , ,与反比例函数的图象相交于点 , ,求 的值.
学习了图形的旋转之后,小明知道,将点 绕着某定点 顺时针旋转一定的角度 ,能得到一个新的点 ,经过进一步探究,小明发现,当上述点 在某函数图象上运动时,点 也随之运动,并且点 的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点 的坐标、角度 的大小来解决相关问题.
【初步感知】
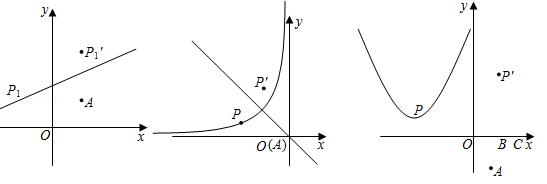
如图1,设 , ,点 是一次函数 图象上的动点,已知该一次函数的图象经过点 .
(1)点 旋转后,得到的点 的坐标为 ;
(2)若点 的运动轨迹经过点 ,求原一次函数的表达式.
【深入感悟】
如图2,设 , ,点 是反比例函数 的图象上的动点,过点 作二、四象限角平分线的垂线,垂足为 ,求 的面积.
【灵活运用】
如图3,设 , ,点 是二次函数 图象上的动点,已知点 、 ,试探究 的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.
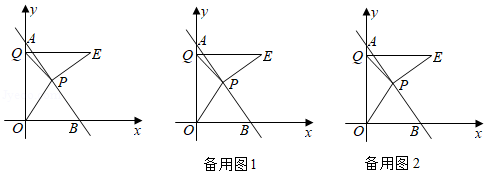
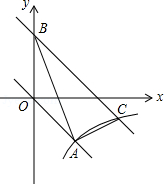
如图,直线 与 轴交于点 ,与 轴交于点 ,点 为线段 的中点,点 是线段 上一动点(不与点 、 重合).
(1)请直接写出点 、点 、点 的坐标;
(2)连接 ,在第一象限内将 沿 翻折得到 ,点 的对应点为点 .若 ,求线段 的长;
(3)在(2)的条件下,设抛物线 的顶点为点 .
①若点 在 内部(不包括边),求 的取值范围;
②在平面直角坐标系内是否存在点 ,使 最大?若存在,请直接写出点 的坐标;若不存在,请说明理由.
如图,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是1.
(1)求 的值;
(2)若将一次函数 的图象向下平移4个单位长度,平移后所得到的图象与反比例函数 的图象相交于 , 两点,求此时线段 的长.
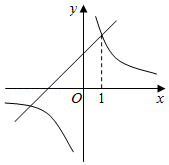
在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位长度得到.
(1)求这个一次函数的解析式;
(2)当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出 的取值范围.
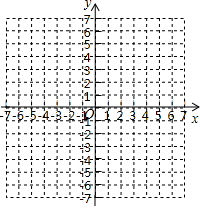
在 中, 边的长为 , 边上的高为 , 的面积为2.
(1) 关于 的函数关系式是 , 的取值范围是 ;
(2)在平面直角坐标系中画出该函数图象;
(3)将直线 向上平移 个单位长度后与上述函数图象有且只有一个交点,请求出此时 的值.
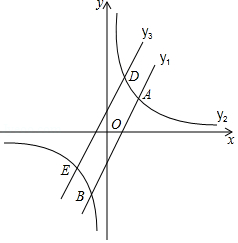
如图,在平面直角坐标系中,直线 与双曲线 交于 、 两点,已知点 ,点 .
(1)求直线和双曲线的解析式;
(2)把直线 沿 轴负方向平移2个单位后得到直线 ,直线 与双曲线 交于 、 两点,当 时,求 的取值范围.
一次函数 的图象经过点 ,且与反比例函数 的图象交于点 .
(1)求一次函数的解析式;
(2)将直线 向上平移10个单位后得到直线 , 与反比例函数 的图象相交,求使 成立的 的取值范围.
如图,把函数 的图象上各点的纵坐标变为原来的2倍,横坐标不变,得到函数 的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
类似地,我们可以认识其他函数.
(1)把函数 的图象上各点的纵坐标变为原来的 倍,横坐标不变,得到函数 的图象;也可以把函数 的图象上各点的横坐标变为原来的 倍,纵坐标不变,得到函数 的图象.
(2)已知下列变化:①向下平移2个单位长度;②向右平移1个单位长度;③向右平移 个单位长度;④纵坐标变为原来的4倍,横坐标不变;⑤横坐标变为原来的 倍,纵坐标不变;⑥横坐标变为原来的2倍,纵坐标不变.
(Ⅰ)函数 的图象上所有的点经过④ ② ①,得到函数 的图象;
(Ⅱ)为了得到函数 的图象,可以把函数 的图象上所有的点 .
.① ⑤ ③ .① ⑥ ③ .① ② ⑥ .① ③ ⑥
(3)函数 的图象可以经过怎样的变化得到函数 的图象?(写出一种即可)

直线 的解析式为 ,分别交 轴、 轴于点 , .
(1)写出 , 两点的坐标,并画出直线 的图象;
(2)将直线 向上平移4个单位得到 , 交 轴于点 .作出 的图象, 的解析式是 .
(3)将直线 绕点 顺时针旋转 得到 , 交 于点 .作出 的图象, .

如图所示,在平面直角坐标系中,直线 与 轴相交于点 与反比例函数 在第一象限内相交于点
(1)求反比例函数的解析式;
(2)将直线 向上平行移动后与反比例函数在第一象限内相交于点 ,且 的面积为4,求平行移动后的直线的解析式.

如图,在平面直角坐标 中,正比例函数 的图象与反比例函数 的图象都经过点 .
(1)分别求这两个函数的表达式;
(2)将直线 向上平移3个单位长度后与 轴交于点 ,与反比例函数图象在第四象限内的交点为 ,连接 , ,求点 的坐标及 的面积.
如图,一次函数的图象与反比例函数
的图象相交,其中一个交点的横坐标是2.
(1)求反比例函数的表达式;
(2)将一次函数的图象向下平移2个单位,求平移后的图象与反比例函数
图象的交点坐标;
(3)直接写出一个一次函数,使其过点,且与反比例函数
的图象没有公共点.