初中数学平面直角坐标系试题

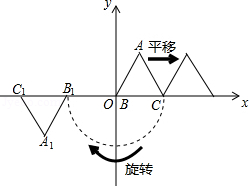
定义：在平面直角坐标系中，一个图形先向右平移 $a$个单位，再绕原点按顺时针方向旋转 $\theta$角度，这样的图形运动叫作图形的 $\gamma (a,\theta )$变换．

如图，等边 $\mathit{\Delta ABC}$的边长为1，点 $A$在第一象限，点 $B$与原点 $O$重合，点 $C$在 $x$轴的正半轴上．△ $A_1{B}_1{C}_1$就是 $\mathit{\Delta ABC}$经 $\gamma (1,180°)$变换后所得的图形．

若 $\mathit{\Delta ABC}$经 $\gamma (1,180°)$变换后得△ $A_1{B}_1{C}_1$，△ $A_1{B}_1{C}_1$经 $\gamma (2,180°)$变换后得△ $A_2{B}_2{C}_2$，△ $A_2{B}_2{C}_2$经 $\gamma (3,180°)$变换后得△ $A_3{B}_3{C}_3$，依此类推 $\dots \dots$

△ $A_{n-1}{B}_{n-1}{C}_{n-1}$经 $\gamma (n,180°)$变换后得△ $A_n{B}_n{C}_n$，则点 $A_1$的坐标是　　，点 $A_{2018}$的坐标是　　．

如图，在平面直角坐标系中，已知 $\odot D$经过原点 $O$，与 $x$轴、 $y$轴分别交于 $A$、 $B$两点， $B$点坐标为 $(0$， $2\sqrt{3})$， $\mathit{OC}$与 $\odot D$交于点 $C$， $\angle \mathit{OCA}=30°$，则图中阴影部分面积为　　．（结果保留根号和 $\pi )$

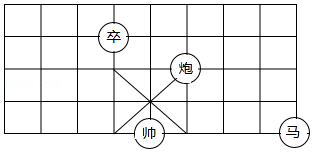
中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱．如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点 $(0,-2)$，“马”位于点 $(4,-2)$，则“卒”位于点　　．

点 $(-1,2)$所在的象限是第　    　象限．

已知正方形的对称中心在坐标原点，顶点 A、 B、 C、 D按逆时针依次排列，若 A点的坐标为（2， $\sqrt{3}$ ），则 B点与 D点的坐标分别为（　　）

A．	（﹣2， $\sqrt{3}$ ），（2，﹣ $\sqrt{3}$ ）	B．	（﹣ $\sqrt{3}$ ，2），（ $\sqrt{3}$ ，﹣2）
C．	（﹣ $\sqrt{3}$ ，2），（2，﹣ $\sqrt{3}$ ）	D．	（- $\frac{\sqrt{7}}{2}$ ， $\frac{\sqrt{21}}{2}$ ）（ $\frac{\sqrt{7}}{2}$ ， $-\frac{\sqrt{21}}{2}$ ）

如图，在平面直角坐标系中，点 $A$的坐标是　　．

如图，在直角坐标系中，点 $A$在函数 $y=\frac{4}{x}(x>0)$的图象上， $\mathit{AB}\perp x$轴于点 $B$， $\mathit{AB}$的垂直平分线与 $y$轴交于点 $C$，与函数 $y=\frac{4}{x}(x>0)$的图象交于点 $D$，连接 $\mathit{AC}$， $\mathit{CB}$， $\mathit{BD}$， $\mathit{DA}$，则四边形 $\mathit{ACBD}$的面积等于 $($　　 $)$

A．2B． $2\sqrt{3}$C．4D． $4\sqrt{3}$

如图，直线 $l$为 $y=\sqrt{3}x$，过点 $A_1(1,0)$作 $A_1{B}_1\perp x$轴，与直线 $l$交于点 $B_1$，以原点 $O$为圆心， $O{B}_1$长为半径画圆弧交 $x$轴于点 $A_2$；再作 $A_2{B}_2\perp x$轴，交直线 $l$于点 $B_2$，以原点 $O$为圆心， $O{B}_2$长为半径画圆弧交 $x$轴于点 $A_3$； $\dots \dots$，按此作法进行下去，则点 $A_n$的坐标为 $($　　 $)$．

一组正方形按如图所示的方式放置，其中顶点 $B_1$在 $y$轴上，顶点 $C_1$、 $E_1$、 $E_2$、 $C_2$、 $E_3$、 $E_4$、 $C_3\dots$在 $x$轴上，已知正方形 $A_1{B}_1{C}_1{D}_1$的边长为1， $\angle B_1{C}_{1}O=60°$， $B_1{C}_1//B_2{C}_2//B_3{C}_3\dots$则正方形 $A_{2016}{B}_{2016}{C}_{2016}{D}_{2016}$的边长是 $($　　 $)$

A． ${\left(\frac{1}{2}\right)}^{2015}$B． ${\left(\frac{1}{2}\right)}^{2016}$C． ${\left(\frac{\sqrt{3}}{3}\right)}^{2016}$D． ${\left(\frac{\sqrt{3}}{3}\right)}^{2015}$

如图，在平面直角坐标系中，点 $A$的坐标是 $(20,0)$，点 $B$的坐标是 $(16,0)$，点 $C$、 $D$在以 $\mathit{OA}$为直径的半圆 $M$上，且四边形 $\mathit{OCDB}$是平行四边形，则点 $C$的坐标为　         　．

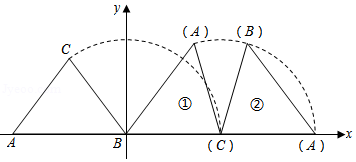
等腰三角形 $\mathit{ABC}$ 在平面直角坐标系中的位置如图所示，已知点 $A(-6,0)$ ，点 $B$ 在原点， $\mathit{CA}=\mathit{CB}=5$ ，把等腰三角形 $\mathit{ABC}$ 沿 $x$ 轴正半轴作无滑动顺时针翻转，第一次翻转到位置①，第二次翻转到位置② $\dots$ 依此规律，第15次翻转后点 $C$ 的横坐标是 　         　．

如图，在平面直角坐标系中，点 $A_1$， $A_2$， $A_3$， $\dots$和 $B_1$， $B_2$， $B_3$， $\dots$分别在直线 $y=\frac{1}{5}x+b$和 $x$轴上．△ $O{A}_1{B}_1$，△ $B_1{A}_2{B}_2$，△ $B_2{A}_3{B}_3$， $\dots$都是等腰直角三角形．如果点 $A_1(1,1)$，那么点 $A_{2018}$的纵坐标是　　．

如图，在直角坐标系中，点 A， B分别在 x轴和 y轴上，点 A的坐标为（﹣2，0），∠ ABO＝30°，线段 PQ的端点 P从点 O出发，沿△ OBA的边按 O→ B→ A→ O运动一周，同时另一端点 Q随之在 x轴的非负半轴上运动，如果 PQ＝2 $\sqrt{\text{3}}$ ，那么当 P点运动一周时，点 Q运动的总路程是（　　）

A．

4 $\sqrt{\text{3}}$

B．

6

C．

6 $\sqrt{\text{3}}$

D．

8

在平面直角坐标系中，点 P（ x， y）经过某种变换后得到点 P'（﹣ y+1， x+2），我们把点 P'（﹣ y+1， x+2）叫做点 P（ x， y）的终结点．已知点 P ₁的终结点为 P ₂，点 P ₂的终结点为 P ₃，点 P ₃的终结点为 P ₄，这样依次得到 P ₁、 P ₂、 P ₃、 P ₄、… P _n、…，若点 P ₁的坐标为（2，0），则点 P ₂₀₁₇的坐标为 　　．

如图，在平面直角坐标系中，已知 A（﹣1，0）， B（0，2），将△ ABO沿直线 AB翻折后得到△ ABC，若反比例函数 y＝ $\frac{k}{x}$ （ x＜0）的图象经过点 C，则 k＝ 　　．