初中数学规律型：图形的变化类试题

将一些半径相同的小圆按如图所示的规律摆放，请仔细观察，第 $n$个图形有　 $(n^2+n+4)$　个小圆．（用含 $n$的代数式表示）

如图，边长为4的等边 $\mathit{\Delta ABC}$， $\mathit{AC}$边在 $x$轴上，点 $B$在 $y$轴的正半轴上，以 $\mathit{OB}$为边作等边 $\mathit{\Delta OB}{A}_1$，边 $O{A}_1$与 $\mathit{AB}$交于点 $O_1$，以 $O_{1}B$为边作等边△ $O_{1}B{A}_2$，边 $O_1{A}_2$与 $A_{1}B$交于点 $O_2$，以 $O_{2}B$为边作等边△ $O_{2}B{A}_3$，边 $O_2{A}_3$与 $A_{2}B$交于点 $O_3$， $\dots$，依此规律继续作等边△ $O_{n-1}B{A}_n$，记△ $O{O}_{1}A$的面积为 $S_1$，△ $O_1{O}_2{A}_1$的面积为 $S_2$，△ $O_2{O}_3{A}_2$的面积为 $S_3$， $\dots$，△ $O_{n-1}{O}_n{A}_{n-1}$的面积为 $S_n$，则 $S_n=$　　． $(n⩾2$，且 $n$为整数）

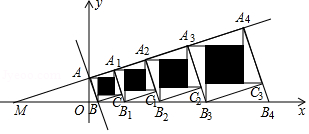
如图，在平面直角坐标系 $\mathit{xOy}$中，直线 $y=-\frac{1}{3}x+\frac{13}{3}$分别与 $x$轴、 $y$轴交于点 $P$、 $Q$，在 $\text{Rt}\Delta \text{OPQ}$中从左向右依次作正方形 $A_1{B}_1{C}_1{C}_2$、 $A_2{B}_2{C}_2{C}_3$、 $A_3{B}_3{C}_3{C}_4\dots A_n{B}_n{C}_n{C}_{n+1}$，点 $A_1$、 $A_2$、 $A_3\dots A_n$在 $x$轴上，点 $B_1$在 $y$轴上，点 $C_1$、 $C_2$、 $C_3\dots C_{n+1}$在直线 $\mathit{PQ}$上；再将每个正方形分割成四个全等的直角三角形和一个小正方形，其中每个小正方形的边都与坐标轴平行，从左至右的小正方形（阴影部分）的面积分别记为 $S_1$、 $S_2$、 $S_3\dots S_n$，则 $S_n$可表示为 $($　　 $)$

A．． $\frac{3^{2n-2}}{4^{2n-3}}$B．． $\frac{3^{n-1}}{4^{n-2}}$

C．． $\frac{3^n}{4^{n-1}}$D．． $\frac{3^{2n}}{4^{2n-1}}$

如图，直线 $y=\frac{1}{3}x+1$与 $x$轴交于点 $M$，与 $y$轴交于点 $A$，过点 $A$作 $\mathit{AB}\perp \mathit{AM}$，交 $x$轴于点 $B$，以 $\mathit{AB}$为边在 $\mathit{AB}$的右侧作正方形 $\mathit{ABC}{A}_1$，延长 $A_{1}C$交 $x$轴于点 $B_1$，以 $A_1{B}_1$为边在 $A_1{B}_1$的右侧作正方形 $A_1{B}_1{C}_1{A}_2\dots$按照此规律继续作下去，再将每个正方形分割成四个全等的直角三角形和一个小正方形，每个小正方形的每条边都与其中的一条坐标轴平行，正方形 $\mathit{ABC}{A}_1$， $A_1{B}_1{C}_1{A}_2$， $\dots$， $A_{n-1}{B}_{n-1}{C}_{n-1}{A}_n$中的阴影部分的面积分别为 $S_1$， $S_2$， $\dots$， $S_n$，则 $S_n$可表示为　　．

小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案（如图所示），每个图案中他只在最下面的正方体上写“心”字，寓意“不忘初心”．其中第（1）个图案中有1个正方体，第（2）个图案中有3个正方体，第（3）个图案中有6个正方体， $\dots$按照此规律，从第 $\left(100\right)$个图案所需正方体中随机抽取一个正方体，抽到带“心”字正方体的概率是 $($　　 $)$

A． $\frac{1}{100}$B． $\frac{1}{20}$C． $\frac{1}{101}$D． $\frac{2}{101}$

如图，正方形 $A_0{B}_0{C}_0{A}_1$的边长为1，正方形 $A_1{B}_1{C}_1{A}_2$的边长为2，正方形 $A_2{B}_2{C}_2{A}_3$的边长为4，正方形 $A_3{B}_3{C}_3{A}_4$的边长为 $8\dots \dots$依此规律继续作正方形 $A_n{B}_n{C}_n{A}_{n+1}$，且点 $A_0$， $A_1$， $A_2$， $A_3$， $\dots$， $A_{n+1}$在同一条直线上，连接 $A_0{C}_1$交 $A_1{B}_1$于点 $D_1$，连接 $A_1{C}_2$交 $A_2{B}_2$于点 $D_2$，连接 $A_2{C}_3$交 $A_3{B}_3$于点 $D_3\dots \dots$记四边形 $A_0{B}_0{C}_0{D}_1$的面积为 $S_1$，四边形 $A_1{B}_1{C}_1{D}_2$的面积为 $S_2$，四边形 $A_2{B}_2{C}_2{D}_3$的面积为 $S_3\dots \dots$四边形 $A_{n-1}{B}_{n-1}{C}_{n-1}{D}_n$的面积为 $S_n$，则 $S_{2019}=$　　．

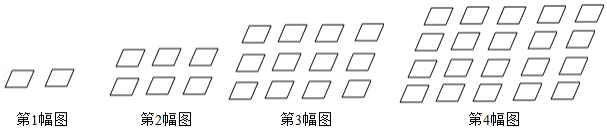
如图所示，将形状大小完全相同的“ $▱$”按照一定规律摆成下列图形，第1幅图中“ $▱$”的个数为 $a_1$，第2幅图中“ $▱$”的个数为 $a_2$，第3幅图中“ $▱$”的个数为 $a_3$， $\dots$，以此类推，若 $\frac{2}{a_1}+\frac{2}{a_2}+\frac{2}{a_3}+\dots +\frac{2}{a_n}=\frac{n}{2020}$． $(n$为正整数），则 $n$的值为　　．

刘莎同学用火柴棒依图的规律摆六边形图案，用10086根火柴棒摆出的图案应该是第　　个．

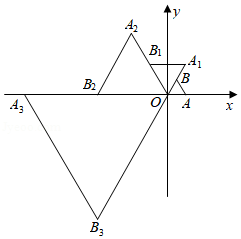
在平面直角坐标系中，等边 $\mathit{\Delta AOB}$ 如图放置，点 $A$ 的坐标为 $(1,0)$ ，每一次将 $\mathit{\Delta AOB}$ 绕着点 $O$ 逆时针方向旋转 $60°$ ，同时每边扩大为原来的2倍，第一次旋转后得到△ $A_{1}O{B}_1$ ，第二次旋转后得到△ $A_{2}O{B}_2$ ， $\dots$ ，依次类推，则点 $A_{2021}$ 的坐标为 $($ 　　 $)$

A．	$(-2^{2020}$ ， $-\sqrt{3}\times 2^{2020})$	B．	$(2^{2021}$ ， $-\sqrt{3}\times 2^{2021})$
C．	$(2^{2020}$ ， $-\sqrt{3}\times 2^{2020})$	D．	$(-2^{2021}$ ， $-\sqrt{3}\times 2^{2021})$

“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．

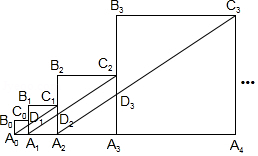
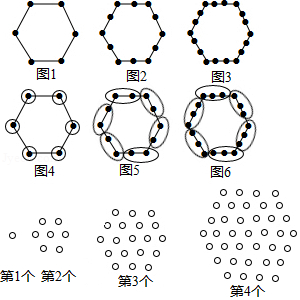
例如：图1有6个点，图2有12个点，图3有18个点， $\dots \dots$，按此规律，求图10、图 $n$有多少个点？

我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是 $6\times 1=6$个；图2中黑点个数是 $6\times 2=12$个：图3中黑点个数是 $6\times 3=18$个； $\dots \dots$；所以容易求出图10、图 $n$中黑点的个数分别是　　、　　．

请你参考以上“分块计数法”，先将下面的点阵进行分块，再完成以下问题：

（1）第5个点阵中有　　个圆圈；第 $n$个点阵中有　　个圆圈．

（2）小圆圈的个数会等于271吗？如果会，请求出是第几个点阵．

如图，在 $\mathit{\Delta ABC}$中， $\mathit{AB}=5$， $\mathit{AC}=4$，若进行以下操作，在边 $\mathit{BC}$上从左到右依次取点 $D_1$、 $D_2$、 $D_3$、 $D_4$、 $\dots$；过点 $D_1$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_1$、 $F_1$；过点 $D_2$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_2$、 $F_2$；过点 $D_3$作 $\mathit{AB}$、 $\mathit{AC}$的平行线分别交 $\mathit{AC}$、 $\mathit{AB}$于点 $E_3$、 $F_3\dots$，则 $4(D_1{E}_1+D_2{E}_2+\dots +D_{2019}{E}_{2019})+5(D_1{F}_1+D_2{F}_2+\dots +D_{2019}{F}_{2019})=$　        　．

如图，正方形 $\mathit{ABCD}$的边长为2，其面积标记为 $S_1$，以 $\mathit{CD}$为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_2$， $\dots$，按照此规律继续下去，则 $S_9$的值为 $($　　 $)$

A． ${\left(\frac{1}{2}\right)}^6$B． ${\left(\frac{1}{2}\right)}^7$C． ${\left(\frac{\sqrt{2}}{2}\right)}^6$D． ${\left(\frac{\sqrt{2}}{2}\right)}^7$

如图，用同样大小的黑色棋子按如图所示的规律摆放：则第⑦个图案有　　个黑色棋子．

问题提出：用若干相同的一个单位长度的细直木棒，按照如图1方式搭建一个长方体框架，探究所用木棒条数的规律．

问题探究：

我们先从简单的问题开始探究，从中找出解决问题的方法．

探究一

用若干木棒来搭建横长是 $m$，纵长是 $n$的矩形框架 $(m$、 $n$是正整数），需要木棒的条数．

如图①，当 $m=1$， $n=1$时，横放木棒为 $1\times (1+1)$条，纵放木棒为 $(1+1)\times 1$条，共需4条；

如图②，当 $m=2$， $n=1$时，横放木棒为 $2\times (1+1)$条，纵放木棒为 $(2+1)\times 1$条，共需7条；

如图③，当 $m=2$， $n=2$时，横放木棒为 $2\times (2+1)$条，纵放木棒为 $(2+1)\times 2$条，共需12条；

如图④，当 $m=3$， $n=1$时，横放木棒为 $3\times (1+1)$条，纵放木棒为 $(3+1)\times 1$条，共需10条；

如图⑤，当 $m=3$， $n=2$时，横放木棒为 $3\times (2+1)$条，纵放木棒为 $(3+1)\times 2$条，共需17条．

问题（一 $)$：当 $m=4$， $n=2$时，共需木棒　　条．

问题（二 $)$：当矩形框架横长是 $m$，纵长是 $n$时，横放的木棒为　　条，

纵放的木棒为　　条．

探究二

用若干木棒来搭建横长是 $m$，纵长是 $n$，高是 $s$的长方体框架 $(m$、 $n$、 $s$是正整数），需要木棒的条数．

如图⑥，当 $m=3$， $n=2$， $s=1$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (1+1)=34$条，竖放木棒为 $(3+1)\times (2+1)\times 1=12$条，共需46条；

如图⑦，当 $m=3$， $n=2$， $s=2$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (2+1)=51$条，竖放木棒为 $(3+1)\times (2+1)\times 2=24$条，共需75条；

如图⑧，当 $m=3$， $n=2$， $s=3$时，横放与纵放木棒之和为 $[3\times (2+1)+(3+1)\times 2]\times (3+1)=68$条，竖放木棒为 $(3+1)\times (2+1)\times 3=36$条，共需104条．

问题（三 $)$：当长方体框架的横长是 $m$，纵长是 $n$，高是 $s$时，横放与纵放木棒条数之和为　　条，竖放木棒条数为　　条．

实际应用：现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架，总共使用了170条木棒，则这个长方体框架的横长是　　．

拓展应用：若按照如图2方式搭建一个底面边长是10，高是5的正三棱柱框架，需要木棒　　条．

如图，小正方形是按一定规律摆放的，下面四个选项中的图片，适合填补图中空白处的是 $($　　 $)$

A．B．C．D．