古希腊数学家定义了五边形数,如下表所示,将点按照表中方式排列成五边形点阵,图形中的点的个数即五边形数;
图形 |
|
|
|
|
|
|
|
五边形数 |
1 |
5 |
12 |
22 |
35 |
51 |
|
将五边形数1,5,12,22,35,51, ,排成如下数表;

观察这个数表,则这个数表中的第八行从左至右第2个数为 .
用m根火柴可以拼成如图1所示的x个正方形,还可以拼成如图2所示的2y个正方形,那么用含x的代数式表示y,得y=_____________.
找规律.一张长方形桌子可坐6人,按下图方式讲桌子拼在一起。

① 2张桌子拼在一起可坐______人;
3张桌子拼在一起可坐______人;
n张桌子拼在一起可坐______人。
② 一家餐厅有40张这样的长方形桌子,按照上图方式每5张桌子拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐______人。
如图:用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n个“口”字需用棋子___个.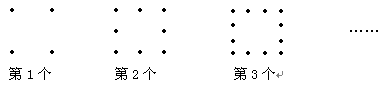
用棋子按如图方式摆图形,依照此规律,第n个图形比第(n -1)个图形多 ▲ 枚棋子.
下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒, ,按此规律,图案⑦需 根火柴棒.

观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2018个图形共有 个〇.

如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为1,则 的半径长是 .

如图,四边形 是正方形,曲线 是由一段段90度的弧组成的.其中: 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; 的圆心为点 ,半径为 ; , 的圆心依次按点 , , , 循环.若正方形 的边长为1,则 的长是 .

已知直线 和直线 ,其中 为不小于2的自然数.
(1)当 时,直线 、 与 轴围成的三角形的面积 ;
(2)当 、3、4, ,2018时,设直线 、 与 轴围成的三角形的面积分别为 , , , , ,则 .
如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍;拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍; 照这样拼图,则第 个图形需要 根火柴棍.
