用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一列图案:
请问第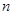 个图案中有白色纸片的张数为
个图案中有白色纸片的张数为
A.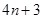 |
B.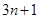 |
C.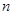 |
D. |
为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆 个“金鱼”需用火柴棒的根数为( )
个“金鱼”需用火柴棒的根数为( )

A. |
B. |
C. |
D. |
为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆 个“金鱼”需用火柴棒的根数为( )
个“金鱼”需用火柴棒的根数为( )

A. |
B. |
C. |
D. |
观察图给出的四个点阵,s表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n个点阵中的点的个数s为( )

| A.3n-2 | B.3n-1 | C.4n+1 | D.4n-3 |
将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图①.在图②中,将骰子向右翻滚 ,然后在桌面上按逆时针方向旋转
,然后在桌面上按逆时针方向旋转 ,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成100次变换后,骰子朝上一面的点数是( )
,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成100次变换后,骰子朝上一面的点数是( )
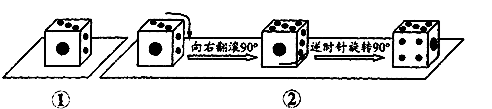
| A.6 | B.5 | C.3 | D.2 |
小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体, 按照此规律,从第 个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是

A. B. C. D.
如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为

A.148B.152C.174D.202
把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形, ,按此规律排列下去,则第⑤个图案中黑色三角形的个数为

A.10B.15C.18D.21
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
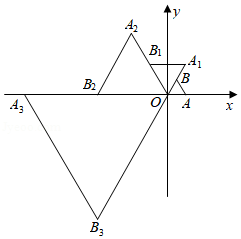
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为( )

| A. |
|
B. |
|
C. |
|
D. |
|
某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图).若有34枚图钉可供选用,则最多可以展示绘画作品

A.16张B.18张C.20张D.21张
利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 ,如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是
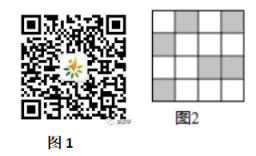
A. B.
B.
C. D.
D.
如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
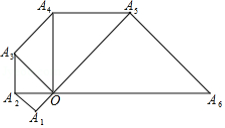
A. B. C. D.