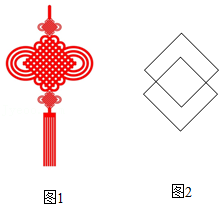
数学兴趣小组同学从"中国结"的图案(图 中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是
| A. |
用3个相同的菱形放置,最多能得到6个菱形 |
| B. |
用4个相同的菱形放置,最多能得到16个菱形 |
| C. |
用5个相同的菱形放置,最多能得到27个菱形 |
| D. |
用6个相同的菱形放置,最多能得到41个菱形 |
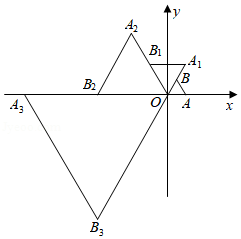
在平面直角坐标系中,等边 如图放置,点 的坐标为 ,每一次将 绕着点 逆时针方向旋转 ,同时每边扩大为原来的2倍,第一次旋转后得到△ ,第二次旋转后得到△ , ,依次类推,则点 的坐标为
| A. |
, |
B. |
, |
| C. |
, |
D. |
, |
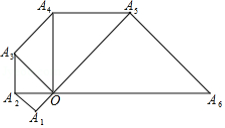
由12个有公共顶点 的直角三角形拼成的图形如图所示, .若 ,则 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
下列图形都是由同样大小的实心圆点按一定规律组成的,其中第①个图形一共有5个实心圆点,第②个图形一共有8个实心圆点,第③个图形一共有11个实心圆点,…,按此规律排列下去,第⑥个图形中实心圆点的个数为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
A. B. C. D.
人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,如图中的每一个小正方形表示一块地砖.如果按图①②③ 的次序铺设地砖,把第 个图形用图 表示,那么第50个图形中的白色小正方形地砖的块数是

A.150B.200C.355D.505
小明用大小和形状都完全一样的正方体按照一定规律排放了一组图案(如图所示),每个图案中他只在最下面的正方体上写“心”字,寓意“不忘初心”.其中第(1)个图案中有1个正方体,第(2)个图案中有3个正方体,第(3)个图案中有6个正方体, 按照此规律,从第 个图案所需正方体中随机抽取一个正方体,抽到带“心”字正方体的概率是

A. B. C. D.
如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为

A.148B.152C.174D.202
把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形, ,按此规律排列下去,则第⑤个图案中黑色三角形的个数为

A.10B.15C.18D.21
某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图).若有34枚图钉可供选用,则最多可以展示绘画作品

A.16张B.18张C.20张D.21张
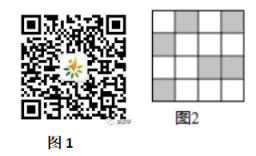
利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 ,如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是
A. B.
B.
C. D.
D.
如图所示,将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形,第1幅图形中“●”的个数为 ,第2幅图形中“●”的个数为 ,第3幅图形中“●”的个数为 , ,以此类推,则 的值为

A. B. C. D.
如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第 个图形中有120朵玫瑰花,则 的值为
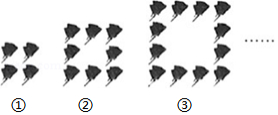
A.28B.29C.30D.31