如图,四边形 是边长为1的正方形,以对角线 为边作第二个正方形 .连接 ,得到△ ;再以对角线 为边作第三个正方形 ,连接 ,得到△ ;再以对角线 为边作第四个正方形,连接 ,得到△ 记△ 、△ 、△ 的面积分别为 、 、 ,如此下去,则 .

如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形 按此规律摆下去,第 个图案有 个三角形(用含 的代数式表示).

归纳“ ”字形,用棋子摆成的“ ”字形如图所示,按照图①,图②,图③的规律摆下去,摆成第 个“ ”字形需要的棋子个数为 .

将一些圆按照如图方式摆放,从上向下有无数行,其中第一行有2个圆,第二行有4个圆,第三行有6个圆 按此规律排列下去,则前50行共有圆 个.

如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成; 按照此规律,第 个图中正方形和等边三角形的个数之和为 个.

如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第 个图案中白色正方形比黑色正方形多 个.(用含 的代数式表示)

如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; ,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 ,如此下去,则 或 .
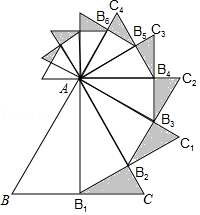
如图,已知等边 的边长是2,以 边上的高 为边作等边三角形,得到第一个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第二个等边△ ;再以等边△ 的 边上的高 为边作等边三角形,得到第三个等边△ ; .记△ 面积为 ,△ 面积为 ,△ 面积为 ,则 .

某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图).若有34枚图钉可供选用,则最多可以展示绘画作品

A.16张B.18张C.20张D.21张
下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转 得到,第2019个图案与第1个至第4个中的第 个箭头方向相同(填序号).

如图,正方形 的边长为1,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,依此下去,第 个正方形的面积为

A. B. C. D.
某广场用同一种如图所示的地砖拼图案,第一次拼成形如图1所示的图案,第二次拼成形如图2所示的图案,第三次拼成形如图3所示的图案,第四次拼成形如图4所示的图案 按照这样的规律进行下去,第 次拼成的图案共用地砖 块.

如图,已知 ,在射线 上取点 ,以 为圆心的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切;在射线 上取点 ,以 为圆心, 为半径的圆与 相切; ;在射线 上取点 ,以 为圆心, 为半径的圆与 相切.若 的半径为1,则 的半径长是 .

利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为 , , , ,那么可以转换为该生所在班级序号,其序号为 ,如图2第一行数字从左到右依次为0,1,0,1,序号为 ,表示该生为5班学生.表示6班学生的识别图案是
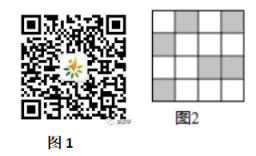
A. B.
B.
C. D.
D.