初中数学计算器—基础知识解答题

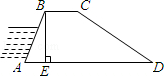
近年来，有私家车的业主越来越多，某小区为解决“停车难”问题，拟建造一个地下停车库．如图是该地下停车库坡道入口的设计示意图，其中水平线AB=10m，BD⊥AB，∠BAD=20°，点C在BD上，BC=1m．根据规定，地下停车库坡道入口上方要张贴限高标志，以提醒驾驶员所驾车辆能否安全驶入．李建认为CD的长度就是限制的高度，而孙杰认为应该以CE的长度作为限制的高度．李建和孙杰谁说的对？请你判断并计算出限制高度．（结果精确到0.1m，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）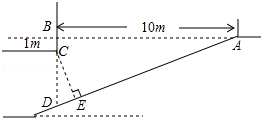

据调查，超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学用所学过的知识在一条笔直的道路上检测车速．如图，观测点C到公路的距离CD为100米，检测路段的起点A位于点C的南偏西60°方向上，终点B位于点C的南偏西45°方向上．某时段，一辆轿车由西向东匀速行驶，测得此车由A处行驶到B处的时间为4秒．问此车是否超过了该路段16米/秒的限制速度？（参考数据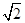：≈1．4，≈1．7）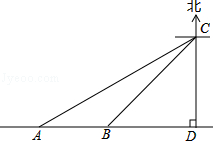

如图，某飞机于空中探测某座山的高度，在点A处飞机的飞行高度是AF=3700米，从飞机上观测山顶目标C的俯角是45°，飞机继续以相同的高度飞行300米到B处，此时观测目标C的俯角是50°，求这座山的高度CD．
（参考数据：sin50°≈0．77，cos50°≈0．64，tan50°≈1．20）．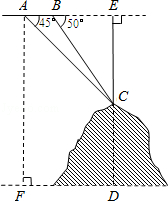

石家庄市某中学举办阳光体育节，开设A：实心球，B：立定跳远，C：跳绳，D：跑步四种活动项目．为了了解学生对四种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图1、图2的统计图，请结合图中的信息解答下列问题：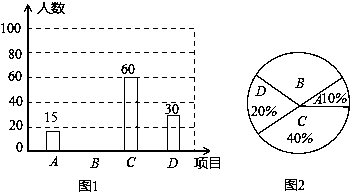

（1）请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比，并将两个统计图补充完整；
（2）若调查到喜欢“跳绳”的5名学生中有3名男生，2名女生，现从这5名学生中任意抽取2名学生，用列表或画树状图的方法，求出刚好抽到同性别学生的概率；
（3）某同学在投实心球过程中某时刻，球和出发点连线与地而成37°角，球距离地面5米，求此时实心球距离出发点多远？（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）

（本题10分） 我市公共自行车项目现已建立了几百个站点，为人们的生活带来了方便．
图（1）所示的是自行车的实物图．图（2）是一辆自行车的部分几何示意图，其中
车架档AC的长为45cm，且∠CAB＝75°，∠CBA=50°．（参考数据：sin75°≈0．96，cos75°≈0．26，tan75°≈3．73 ，sin50°≈0．76，cos50°≈0．64，tan50°≈1．19）
 
（1）求车座固定点C到车架档AB的距离；
（2）求车架档AB的长（第2小题结果精确到1cm）．

如图，A、B是两座现代化城市，C是一个古城遗址，C城在A城的北偏东30°方向，在B城的北偏西45°方向，且C城与A城相距120千米，B城在A城的正东方向，以C为圆心，以60千米为半径的圆形区域内有古迹和地下文物，现要在A、B两城市间修建一条笔直的高速公路．

（1）请你计算公路的长度．（结果保留根号）
（2）请你分析这条公路有没有可能是对古迹或文物赞成损毁．

如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的长度是12．5米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角∠CAQ为45°，坡角∠BAQ为37°，求二楼的层高BC（精确到0．1米）．（参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75 ）

如图，某建筑物BC上有一旗杆AB，小明在F处，由E点观察到旗杆顶部A的仰角为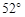，底部B的仰角为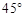，小明的观测点与地面距离EF为1．6m，

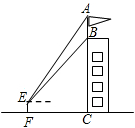
（1）若F与BC相距12m，求建筑物BC的高度；
（2）若旗杆AB长3．15m，求建筑物BC的高度．（结果精确到0．1m）（参考数据：4 ，）．

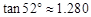如图，三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航，某一时刻航行到A处，测得该岛在北偏东30°方向，海监船以20海里/时的速度继续航行，2小时后到达B处，测得该岛在北偏东75°方向，求此时海监船与黄岩岛P的距离BP的长．（参考数据：≈1．414，结果精确到0．1）

已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．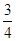

（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．

关于三角函数有如下的公式：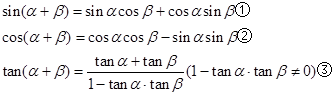

利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：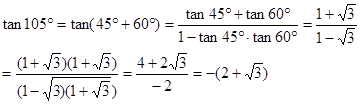

根据上面的知识，你可以选择适当的公式解决下面实际问题：
如图所示，直升机在一建筑物CD上方A点处测得建筑物顶端D点的俯角为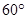，底端C点的俯角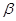为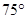，此时直长机与建筑物CD的水平距离BC为42米，求建筑物CD的高。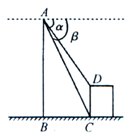

如图，一扇窗户垂直打开，即OM⊥OP，AC是长度不变的滑动支架，其中一端固定在窗户的点A处，另一端在OP上滑动，将窗户OM按图示方向向内旋转35°到达ON位置，此时，点A、C的对应位置分别是点B、D．测量出∠ODB为25°，点D到点O的距离为30cm．

（1）求B点到OP的距离；
（2）求滑动支架的长．
（结果精确到1cm．参考数据：sin25°≈0．4，cos25°≈0．9，tan25°≈0．5，sin55°≈0．8，cos55°≈0．6，tan55°≈1．4）

如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0．1m）．（参考数据：≈1．414，≈1．732）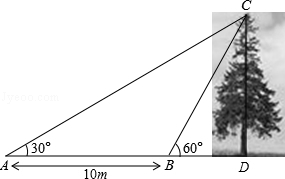

如图，某河堤的横断面是梯形ABCD，BC∥AD，BE⊥AD于点E，AB=50米，BC=30米，∠A=60°，∠D=30°．求AD的长度．

（1）计算：（1-）⁰-tan60°+（）^-1   
（2）解方程组：．