初中数学计算器—基础知识解答题

小明坐于堤边垂钓，如图，河堤AC的坡角为30°，AC长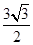米，钓竿AO的倾斜角是60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．

如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的长度是12．5米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角∠CAQ为45°，坡角∠BAQ为37°，求二楼的层高BC（精确到0．1米）．（参考数据：sin37°≈0．60，cos37°≈0．80，tan37°≈0．75 ）

如图，在马航失联客机“MH370”搜寻中需要确定疑似海面上油污带AB的长度．已知在离地面1500m高度C处的飞机上，测量人员测得正前方A、B两点处的俯角分别为60°和45°．求油污带AB的长．（参考数据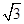：=1．73）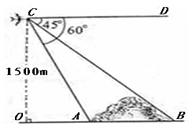

如图，某建筑物BC上有一旗杆AB，小明在F处，由E点观察到旗杆顶部A的仰角为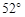，底部B的仰角为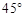，小明的观测点与地面距离EF为1．6m，

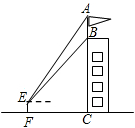
（1）若F与BC相距12m，求建筑物BC的高度；
（2）若旗杆AB长3．15m，求建筑物BC的高度．（结果精确到0．1m）（参考数据：4 ，）．

（1）计算：
（2）先化简，再求值：，请代入一个你喜欢的值并进行计算．

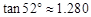如图，三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航，某一时刻航行到A处，测得该岛在北偏东30°方向，海监船以20海里/时的速度继续航行，2小时后到达B处，测得该岛在北偏东75°方向，求此时海监船与黄岩岛P的距离BP的长．（参考数据：≈1．414，结果精确到0．1）

（1）解方程：；
（2）计算：

已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．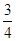

（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．

已知，如图，△ABC中．AD⊥BC于D，AC=10，BC=21，△ABC面积为84，求sinBcosC+cosBsinC的值．

如图，一扇窗户垂直打开，即OM⊥OP，AC是长度不变的滑动支架，其中一端固定在窗户的点A处，另一端在OP上滑动，将窗户OM按图示方向向内旋转35°到达ON位置，此时，点A、C的对应位置分别是点B、D．测量出∠ODB为25°，点D到点O的距离为30cm．

（1）求B点到OP的距离；
（2）求滑动支架的长．
（结果精确到1cm．参考数据：sin25°≈0．4，cos25°≈0．9，tan25°≈0．5，sin55°≈0．8，cos55°≈0．6，tan55°≈1．4）

关于三角函数有如下的公式：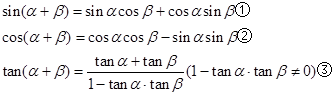

利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：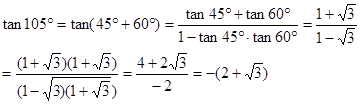

根据上面的知识，你可以选择适当的公式解决下面实际问题：
如图所示，直升机在一建筑物CD上方A点处测得建筑物顶端D点的俯角为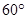，底端C点的俯角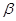为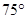，此时直长机与建筑物CD的水平距离BC为42米，求建筑物CD的高。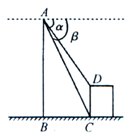

如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0．1m）．（参考数据：≈1．414，≈1．732）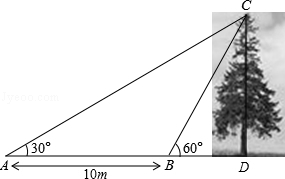

如图，某河堤的横断面是梯形ABCD，BC∥AD，BE⊥AD于点E，AB=50米，BC=30米，∠A=60°，∠D=30°．求AD的长度．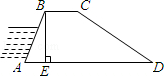

（1）计算：（1-）⁰-tan60°+（）^-1   
（2）解方程组：．

某天早晨，小王从家出发，骑摩托车前往工厂上班，途中在路旁一家饭店吃早餐，如图所示的是小王从家到工厂这一过程中行驶路程 s（千米）与时间t之间的关系．
（1）工厂离小王家多远？从家出发到工厂，小王共用了多少时间？
（2）小王吃早餐用了多少时间？
（3）小王吃早餐以前的速度快还是吃完早餐以后的速度快？最快时速达到多少？