江苏省盐城市盐都区九年级上学期期末考试数学试卷
⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
| A.相切 | B.相交 | C.相离 | D.不能确定 |
一个布袋里装有5个球,其中3个红球,2个白球,每个球除颜色外其他完全相同,从中任意摸出一个球,是红球的概率是( )
A.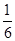 |
B.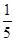 |
C.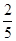 |
D. |
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比为 ( )
| A.1:2 | B.2:1 | C.1:4 | D.4:1 |
如图,AB是⊙O的直径,C.D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠BOC=( )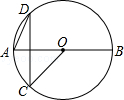
A.25° B.50° C.130° D.155°
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
| A.(60°,4) | B.(45°,4) | C.(60°, ) ) |
D.(50°, ) ) |
如果在比例尺为1:1 000 000的地图上,A.B两地的图上距离是3.4cm,那么A、B两地的实际距离是 km.
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为 _m.
如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°,则该圆锥的母线长l为 cm.
在二次函数 中,函数y与自变量x的部分对应值如下表:
中,函数y与自变量x的部分对应值如下表:
则m、n的大小关系为 m_ _n.(填“<”,“=”或“>”)
已知Rt△ABC中,∠C=90°,BC=1,AC=4,如图把边长分别为x1,x2,x3,…,xn的n个正方形依次放入△ABC中,则第2015个正方形的边长为_ _.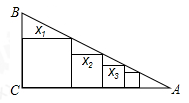
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(―2,1),B(-1,4),C(-3,2).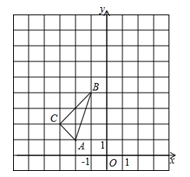
(1)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点坐标;
(2)如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)计算两队决赛成绩的平均数;
(2)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
甲、乙两人用如图的两个分格均匀的转盘A、B做游戏,游戏规则如下:分别转动两个转盘,转盘停止后,指针分别指向一个数字(若指针停止在等份线上,那么重转一次,直到指针指向某一数字为止).用所指的两个数字相乘,如果积是奇数,则甲获胜;如果积是偶数,则乙获胜.请你解决下列问题:
(1)用列表格或画树状图的方法表示游戏所有可能出现的结果.
(2)求甲、乙两人获胜的概率.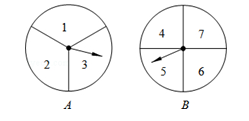
盐城公共自行车项目现已全部建成,盐城市区250个站点,累计投放6000辆自行车,为人们的生活带来了方便.图(1)所示的是自行车的实物图.图(2)是一辆自行车的部分几何示意图,其中车架档AC的长为45cm,且∠CAB=75°,∠CBA=50°.(参考数据:sin75°≈0.96,cos75°≈0.26,tan75°≈3.73 ,sin50°≈0.76,cos50°≈0.64,tan50°≈1.19)
(1)求车座固定点C到车架档AB的距离;
(2)求车架档AB的长(结果精确到1cm).
已知二次函数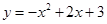 .
.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当―2<x<2时,函数值y的取值范围.
如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC相切于点D.若BE=6,BD=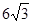 .
.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
某商店将成本为30元的文化衫标价50元出售.
(1)为了搞促销活动经过两次降价调至每件40.5元,若两次降价的百分率相同,求每次降价的百分率;
(2)经调查,该文化衫每降5元,每月可多售出100件,若该品牌文化衫按原标价出售,每月可销售200件,那么销售价定为多少元,可以使该商店获得最大的利润?最大利润是多少?
【问题背景】
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2.我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.
【问题探究】
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为_ _.
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G.将∠AEG绕点A顺时针旋转30°得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′,C′分别在直线l2,l4上,求菱形AB′C′D′的边长.



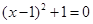
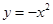 向上平移2个单位后,得到的函数表达式是( )
向上平移2个单位后,得到的函数表达式是( )

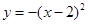


 (
( )的一个解是
)的一个解是 ,则
,则 的值是 .
的值是 . ;
;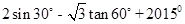
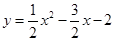 的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
的图像与x轴交于点A,B.点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号