初中数学计算器—基础知识解答题

如图，三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航，某一时刻航行到A处，测得该岛在北偏东30°方向，海监船以20海里/时的速度继续航行，2小时后到达B处，测得该岛在北偏东75°方向，求此时海监船与黄岩岛P的距离BP的长．（参考数据：≈1．414，结果精确到0．1）

某教师的月工资数与工作的年数如下表所示（工资单位：元）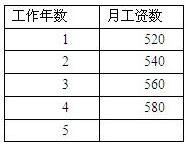

（1）填出第5年他的月工资数；
（2）用含n的代数式表示他第n年的月工资数；
（3）用（2）的代数式求该教师工作第17年的
工资数．

（1）解方程：；
（2）计算：

直线y=－x+6与坐标轴分别交于A、B两点，动点P、Q同时从O点匀速出发，同时到达A点时运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．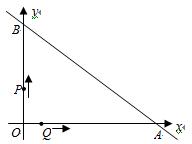

直接写出A、B两点的坐标；
设点Q的运动时间为t秒，△OPQ的面积为S，求出S与t之间的函数关系式；
当s= 时，求出点P的坐标，并直接写出以点O、P、Q为顶点的平行四边形的
第四个顶点M的坐标．

已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A，C的坐标分别为A（﹣3，0），C（1，0），tan∠BAC=．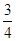

（1）写出点B的坐标；
（2）在x轴上找一点D，连接BD，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；
（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请求出的m值；如不存在，请说明理由．

一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。
请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t（h）之间的函数关系式；
该蜡烛可点燃多长时间？

已知，如图，△ABC中．AD⊥BC于D，AC=10，BC=21，△ABC面积为84，求sinBcosC+cosBsinC的值．

如图1，已知抛物线的顶点为，且经过原点，与轴的另一个交点为．
求抛物线的解析式；
若点在抛物线的对称轴上，点在抛物线上，且以、、、四点为顶点的四边形为平行四边形，求点的坐标；
连接、，如图2，在轴下方的抛物线上是否存在点，使得 与相似？若存在，求出点的坐标；若不存在，说明理由．

如图，一扇窗户垂直打开，即OM⊥OP，AC是长度不变的滑动支架，其中一端固定在窗户的点A处，另一端在OP上滑动，将窗户OM按图示方向向内旋转35°到达ON位置，此时，点A、C的对应位置分别是点B、D．测量出∠ODB为25°，点D到点O的距离为30cm．

（1）求B点到OP的距离；
（2）求滑动支架的长．
（结果精确到1cm．参考数据：sin25°≈0．4，cos25°≈0．9，tan25°≈0．5，sin55°≈0．8，cos55°≈0．6，tan55°≈1．4）

某天早晨，小王从家出发，骑摩托车前往工厂上班，途中在路旁一家饭店吃早餐，如图所示的是小王从家到工厂这一过程中行驶路程 s（千米）与时间t之间的关系．
（1）工厂离小王家多远？从家出发到工厂，小王共用了多少时间？
（2）小王吃早餐用了多少时间？
（3）小王吃早餐以前的速度快还是吃完早餐以后的速度快？最快时速达到多少？

关于三角函数有如下的公式：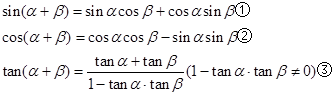

利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值，如：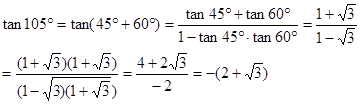

根据上面的知识，你可以选择适当的公式解决下面实际问题：
如图所示，直升机在一建筑物CD上方A点处测得建筑物顶端D点的俯角为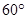，底端C点的俯角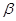为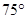，此时直长机与建筑物CD的水平距离BC为42米，求建筑物CD的高。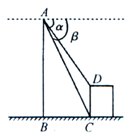

如图，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10m，到达B点，在B处测得树顶C的仰角高度为60°（A、B、D三点在同一直线上）．请你根据他们测量数据计算这棵树CD的高度（结果精确到0．1m）．（参考数据：≈1．414，≈1．732）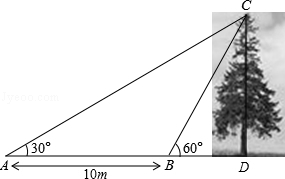

如图，某河堤的横断面是梯形ABCD，BC∥AD，BE⊥AD于点E，AB=50米，BC=30米，∠A=60°，∠D=30°．求AD的长度．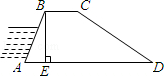

（1）计算：（1-）⁰-tan60°+（）^-1   
（2）解方程组：．

小丽驾车从甲地到乙地。设她出发第x min时的速度为y km/h，图中的折线表示她在整个驾车过程中y与x之间的函数关系。

（1）小丽驾车的最高速度是        km/h；
（2）当20£x£30时，求y与x之间的函数关系式，并求出小丽出发第22 min时的速度；
（3）如果汽车每行驶100 km耗油10 L，那么小丽驾车从甲地到乙地共耗油多少升？