初中数学计算器—基础知识解答题

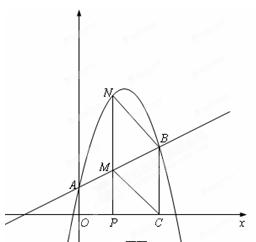
如图，抛物线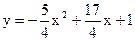与y轴交于A点，过点A的直线与抛物线交于另一点B，过点B作BC⊥x轴，垂足为点C(3，0).
求直线AB的函数关系式；
动点P在线段OC上从原点出发以每秒一个单位的速度向C移动，过点P作PN⊥x轴，交直线AB于点M，交抛物线于点N. 设点P移动的时间为t秒，MN的长度为s个单位，求s与t的函数关系式，并写出t的取值范围；
设在（2）的条件下（不考虑点P与点O，点C重合的情况），连接CM，BN，当t为何值时，四边形BCMN为平行四边形？问对于所求的t值，平行四边形BCMN是否菱形？请说明理由.

如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．
在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；
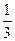在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．

平面直角坐标系中,顺次连结(-2,1),(-2,-1),(2,-2),(2,3)各点,你会得到
一个什么图形?试求这个图形的面积.

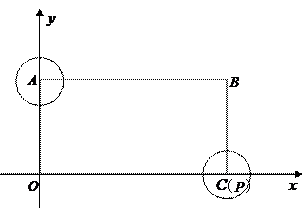
如图11，正比例函数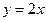的图像与一次函数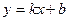的图像交于点A(ｍ，2)， 一次函数图像经过点B 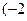, 与y轴的交点为C与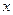轴的交点为D．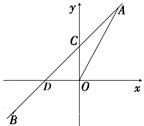

（1）求一次函数解析式；
（2）求C点的坐标；
（3）求△AOD的面积。

某企业信息部进行市场调研发现：
信息一：如果单独投资A种产品，所获利润yＡ(万元)与投资金额x(万元)之间存在某种关系的部分对应值如下表：

x(万元)	1	2	2.5	3	5
yＡ(万元)	0.4	0.8	1	1.2	2

信息二：如果单独投资B种产品，则所获利润yＢ(万元)与投资金额x(万元)之间存在二次函数关系：yＢ＝ax2+bx，且投资2万元时获利润2.4万元，当投资4万元时，可获利润3.2万元．
(1)求出yＢ与x的函数关系式．
(2)从所学过的一次函数、二次函数、反比例函数中确定哪种函数能表示yＡ与x之间的关系，并求出yＡ与x的函数关系式．
(3)如果企业同时对A、B两种产品共投资15万元，请设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？

已知函数，试研究该函数的性质．

每个小方格都是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系中的位置如图所示。

（1）将菱形OABC先向右平移4个单位，再向上平移2个单位，得到菱形O1A1B1C1，请画出菱形O1A1B1C1；
（2）将菱形OABC绕原点O顺时针旋转90º，得到菱形OA2B2C2，请画出菱形OA2B2C2，并写出点A2、B2、C2三点的坐标

如图，在平面直角坐标系中，四边形ABCD的四个顶点的坐标分别是A（1，3）、
B（2，2）、C（2，1），D（3，3）．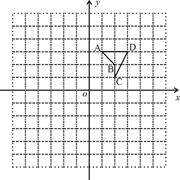

（1）以原点O为位似中心，相似比为2，将图形放大，画出符合要求的位似四边形；
（2）在（1）的前提下，写出点A的对应点坐标A′

如图,在平面直角坐标系中,A(-3,0)，点C在y轴的正半轴上，BC∥x轴，且BC=5,AB交y轴于点D，OD=．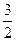

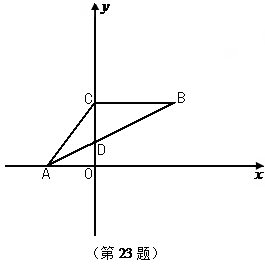
（1）求出点C的坐标；
（2）过A、C、B三点的抛物线与x轴交于点E，连接BE．若动点M从点A出发沿x轴向x轴正方向运动，同时动点N从点E出发，在直线EB上作匀速运动，两个动点的运动速度均为每秒1个单位长度，请问当运动时间t为多少秒时，△MON为直角三角形?

某工厂有甲、乙两个蓄水池，将甲池中的水以每小时5立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y（米）与注水时间x（时）之间的函数图象如图所示，结合图象回答下列问题：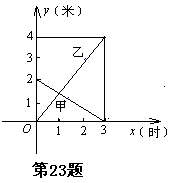

（1）分别求出甲、乙两个蓄水池中水的深度y（米）与注水时间x（时）之间的函数关系式（不写自变量x的取值范围）；
（2）算出注水多长时间后甲、乙两个蓄水池水的深度相同？  
（3）当两个蓄水池水深相同时，水深是多少？并求出甲蓄水池刚开始里面的蓄水量是多少立方米？

已知点P（x，y）是第一象限内的一个动点，且满足x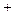y="4. " 请先在所给的平面直角坐标系中画出函数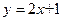的图象，该图象与x轴交于点A，然后解答下列问题：

（1）利用所画图象，求当－1≤y≤3时x的取值范围；
（2）若点P正好也在直线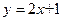上，求点P的坐标；
（3）设△OPA的面积为S，求S关于点P的横坐标x的函数解析式．

如图，A、B两点的坐标分别是A、B．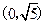

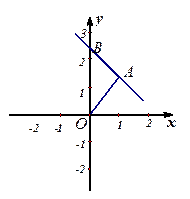
（1）求△OAB的面积；
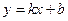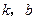（2）若过A、B两点的直线解析式为，求的值.
（本小题结果保留小数点后一位）