广东省天河区初二上学期期末数学卷
甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅要他们拿卷尺帮助检测一个窗框的形状是否是矩形,他们各自做了如下检测,你认为最有说服力的是
| A.甲量得窗框的一组邻边相等 |
| B.乙量得窗框两组对边分别相等 |
| C.丙量得窗框的对角线长相等 |
| D.丁量得窗框的两组对边分别相等且两条对角线也相等 |
某公司把500万元资金投入新产品的生产,第一年获得一定的利润,在不抽掉资金和利润的前提下,继续生产,第二年的利润率提高8%,若第二年的利润达到112万元,设第一年的利润率为x,则可列方程为
| A.500(1+x)(1+x+8%)=112 | B.500(1+x)(1+x+8%)="112" +500 |
| C.500(1+x)·8%=112 | D.500(1+x)(x+8%)=112 |
观察下列各式: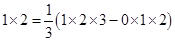

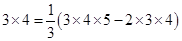
……
计算:3×(1×2+2×3+3×4+…+100×101)=
| A.97×98×99 | B.98×99×100 | C.99×100×101 | D.100×101×102 |
△ABC中,AB=AC,AB的中垂线交边AC于D,若△ABC的周长比△BCD的周长大3cm,则你可以求得哪条线段的长?是多少?
(直接写出结论) _________________
(8分)
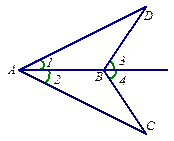
如图,AD平分∠MAN, BD⊥AM,CD⊥AN,垂足分别为B、C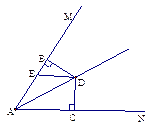
(1)说明:AB=AC
(2)若点E为线段AB上一点,用尺规在射线AN上找一点F,使△CDF与△BDE全等(保留作图痕迹),请写出此时∠AFD与∠AED的关 系,并说明理由.
系,并说明理由.
(8分)
如图,一个被两条直径分成4个扇形的圆形转盘(两条直径的一个夹角为60°),其中3个扇形分别标有数字3,4,5,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(如果指针指向两个扇形的交线时,那么重转1次,直到指针指向某一扇形的位置).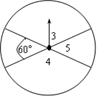
(1)求当转动这个转盘,转盘自由停止后,指针指向没有标数字的扇形的概率;
(2)请在6,7这2个数字中选出一个数字填写在没有标数字的扇形内,使得分别转动转盘2次,转盘自由停止后指针所指扇形的数字和分别为奇数与为偶数的概率相等,并说明理由
某宾馆有若干间住房,住宿记录提供了如下信息:①10月5日全部住满,一天住宿费收入为12000元;②10月6日有20间房空着,一天住宿费收入为9600元;③该宾馆每间房每天收费标准相同.
(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
(2)10月份以后,通过市场调查发现,每间住房每天的定价每增加10元,该宾馆的所有房间就会有5个房间空闲;己知该宾馆空闲房间每天每间支出费用10元,有游客居住房间每天每间支出费用20元,问房价定为多少元时,该宾馆一天的利润为11000元?
(利润=住宿费收入-支出费用)
(12分) 阅读并解答问题
用配方法可以解一元二次方程,还可以用它来解决很多问题.例如:因为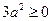 ,所以
,所以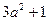 就有最小值1,即
就有最小值1,即 ,只有当
,只有当 时,才能得到这个式子的最小值1.同样,因为
时,才能得到这个式子的最小值1.同样,因为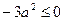 ,所以
,所以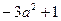 有最大值1,即
有最大值1,即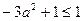 ,只有在
,只有在 时,才能得到这个式子的最大值1.
时,才能得到这个式子的最大值1.
(1)当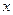 = 时,代数式
= 时,代数式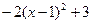 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当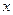 = 时,代数式
= 时,代数式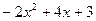 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
(12分)
已知在菱形ABCD中,E是BC的中点,且∠FAE=∠BAE.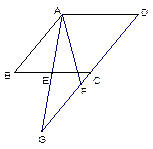
(1) 如图,当点F在边DC的延长线上时,求证:AF=BC-CF;
(2)  当点F与点C重合时,求∠B的度数,并说明理由;
当点F与点C重合时,求∠B的度数,并说明理由;
(3) 当点F在边DC上时,(1)中求证的结论还成立吗?若不成立,
请直接写出成立的结论;
(4)当∠B=90°时,请确定点F的位置
下列各运算中,正确的运算是( )
A.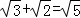 |
B.(﹣2a3)2=4a6 | C.a6÷a2=a3 | D.(a﹣3)2=a2﹣9 |
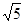 是一个无理数,则下列判断正确的是( ).
是一个无理数,则下列判断正确的是( ).
A.1<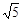 -1<2 -1<2 |
B.2<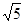 -1< 3 -1< 3 |
C.3<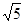 -1<4 -1<4 |
D.4<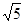 -1<5 -1<5 |
在一定条件下,若物体运动的路程S(米)与时间t(秒)的关系式为S=5t2+2t,则当t=4秒时,该物体所经过的路程为( ).
| A.28米 | B.48米 | C.68米 | D.88米 |
对x2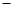 3x
3x 2分解因式的结果为( )
2分解因式的结果为( )
A.x(x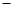 3) 3) 2 2 |
B.(x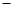 1)(x 1)(x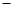 2) 2) |
C.(x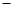 1)(x 1)(x 2) 2) |
D.(x 1)(x 1)(x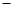 2) 2) |
随着海拔高度的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量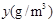 与大气压强x(kpa)成正比例函数关系.当
与大气压强x(kpa)成正比例函数关系.当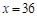 时,
时,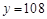 ,则
,则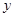 与
与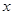 的函数关系式是
的函数关系式是
如图,△ABC≌△DCB,A、B的对应顶点分别为点D、C,如果AB=7cm,BC=12cm,AC=9cm,DO=2cm,那么OC的长是 cm.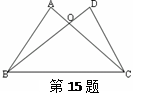
如图,A、B两点的坐标分别是A 、B
、B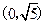 .
.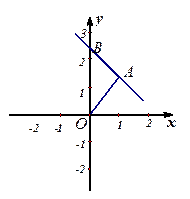
(1)求△OAB的面积;
(2)若过A、B两点的直线解析式为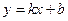 ,求
,求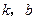 的值.
的值.
(本小题结果保留小数点后一位)
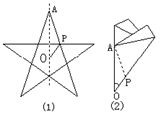
如图,四边形ABCD是长方形.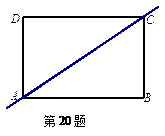
(1)作△ABC关于直线AC对称的图形;
(2)试判断(1)中所作的图形与△ACD重叠部分的三角形形状,并说明理由.
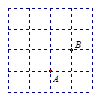
已知点P(x,y)是第一象限内的一个动点,且满足x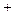 y="4. " 请先在所给的平面直角坐标系中画出函数
y="4. " 请先在所给的平面直角坐标系中画出函数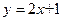 的图象,该图象与x轴交于点A,然后解答下列问题:
的图象,该图象与x轴交于点A,然后解答下列问题:
(1)利用所画图象,求当-1≤y≤3时x的取值范围;
(2)若点P正好也在直线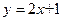 上,求点P的坐标;
上,求点P的坐标;
(3)设△OPA的面积为S,求S关于点P的横坐标x的函数解析式.
已知:如图,AB=AC,点D是BC的中点,AB平分∠DAE,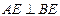 ,垂足为E.
,垂足为E.
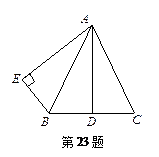
(1)求证:AD=AE.
(2)若BE∥AC,试判断△ABC的形状,并说明理由.
(本小题满分12分)
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x(单位:分)如图2所示.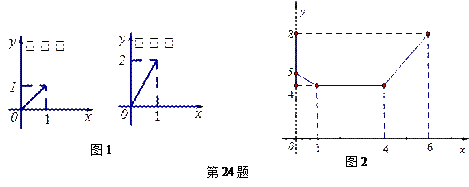
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
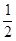
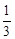
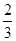
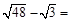
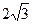
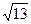 .(填“>”、“=”、
.(填“>”、“=”、 “<”)
“<”) 的方程
的方程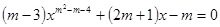 是一元二次方程,则
是一元二次方程,则 =
=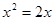 的解为
的解为 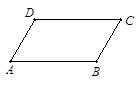
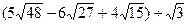

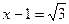 ,求代数式
,求代数式 的值
的值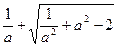 ,其中
,其中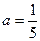 ”的解答是:
”的解答是: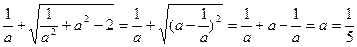 ,
,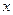 的方程
的方程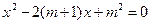 .
.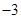

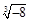 的绝对值是( ).
的绝对值是( ).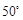
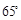
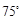

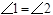 ,
,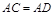 ,增加下列条件:①
,增加下列条件:①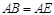 ;②
;②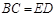 ;③
;③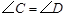 ;④
;④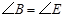 .其中能使
.其中能使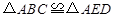 的条件有( ).
的条件有( ).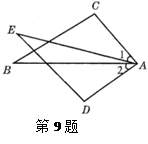
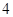 个
个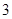 个
个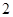 个
个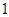 个
个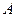 ,且与正比例函数
,且与正比例函数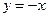 的图象交于点
的图象交于点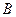 ,则该一次函数的表达式为( )
,则该一次函数的表达式为( )
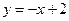
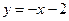
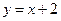
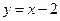
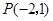 关于
关于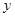 轴的对称点的坐标为
轴的对称点的坐标为 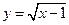 有意义,则自变量
有意义,则自变量 的取值范围是
的取值范围是 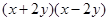 =
= 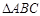 中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD=
中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD= 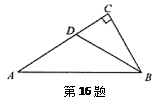
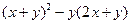
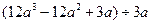
 1的平方根为±5,求5x+4的立方根.
1的平方根为±5,求5x+4的立方根.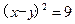 ,求xy的值.
,求xy的值.
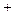 BD=AC,求∠B︰∠C 的比值
BD=AC,求∠B︰∠C 的比值 粤公网安备 44130202000953号
粤公网安备 44130202000953号