(本小题满分12分)
一个安装了两个进水管和一个出水管的容器,每分钟的进水量和出水量是两个常数,且两个进水管的进水速度相同. 进水管和出水管的进出水速度如图1所示,某时刻开始到6分钟(至少打开一个水管),该容器的水量y(单位:升)与时间x(单位:分)如图2所示.
(1)试判断0到1分、1分到4分、4分到6分这三个时间段的进水管和出水管打开的情况.
(2)求4≤x≤6时,y随x变化的函数关系式.
(3)6分钟后,若同时打开两个水管,则10分钟时容器的水量是多少升?
相关知识点
推荐套卷
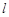 经过点A(1,0),与双曲线
经过点A(1,0),与双曲线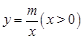 交于点B(2,1).过点P(
交于点B(2,1).过点P(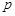 ,
,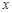 轴的平行线分别交双曲线
轴的平行线分别交双曲线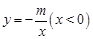 于点M、N.
于点M、N.
 的值;
的值;
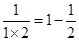 ;
;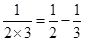 ;
;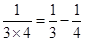 ;……
;……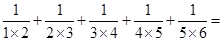 .
.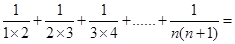 .(用含有
.(用含有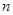 的式子表示)
的式子表示)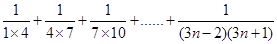 的值为
的值为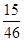 ,求
,求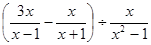 ,再从不等式组
,再从不等式组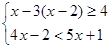 的解集中取一个合适的值代人,求原分式的值.
的解集中取一个合适的值代人,求原分式的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号