如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后,小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°.重力加速度大小为g。若ω=ω0,小物块受到的摩擦力恰好为零,求ω0;
如图所示,一个人用一根长为R=1米,能承受最大拉力为F=74N的绳子,系着一个质量为m=1Kg的小球,在竖直平面内作圆周运动,已知圆心O离地面高h=6米。运动中小球在圆周的最低点时绳子刚好被拉断,绳子的质量和空气阻力均忽略不计,g="10" m/s2.求:
(1)绳子被拉断的瞬间,小球的速度v的大小?
(2)绳断后,小球落地点与圆周的最低点间的水平距离x多大?
如图所示。一端连着质量为m的小球的、长为L的轻杆另一端连在水平光滑轴O上,可在竖直面内转动。当小球运动至最高点A时,杆对小球的支持力大小为mg/2,则当小球运动至最低点B时,杆对小球的拉力大小为多少?
如图,一个质量为0.6kg 的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=0.3m ,θ="60" 0,小球到达A点时的速度 v="4" m/s 。(取g ="10" m/s2)求: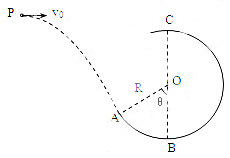
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直高度;
(3)小球到达圆弧最高点C时对轨道的压力。
如图所示,在倾角为37°的固定斜面上静置一个质量为5 kg的物体,物体与斜面间的动摩擦因数为0.8。sin 37°=0.6,cos 37°=0.8。求:
(1)物体所受的摩擦力;
(2)若用原长为10 cm,劲度系数为3.1×103 N/m的弹簧沿斜面向上拉物体,使之向上匀速运动,则弹簧的最终长度是多少?取g="10" m/s2
汽车从制动到停下共用了6s时间,在这段时间内,汽车门1s前进的距离分别是11m、9m、7m、5m、3m、1m.
求汽车前1S、前2S、前3S、和全程的平均速度。
求汽车停止前最后两秒的平均速度
汽车关闭油门时的速度最接近上述两问中的哪个速度?关闭油门时的速度比这个速度偏大还是偏小?
如图所示,质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连,弹簧的劲度系数为k,一条不可伸长的轻绳绕过定滑轮,一端连物体A,另一端连一质量为m的物体C,物体A、B、C都处于静止状态.已知重力加速度为g,忽略一切摩擦.
(1)求物体B对地面的压力;
(2)把物体C的质量改为5m,这时C缓慢下降,经过一段时间系统达到新的平衡状态,这时B仍没离开地面,且C只受重力和绳的拉力作用,求此过程中物体A上升的高度.
如图所示,倾角为θ的斜面固定于电梯中,当电梯加速度为a竖直向上加速运动时,质量为m的物体始终与斜面保持相对静止,则物体受到的支持力和摩擦力是多大?
某同学表演魔术时,将一小型条形磁铁藏在自己的袖子里,然后对着一悬挂的金属小球指手画脚,结果小球在他神奇的功力下飘动起来.假设当隐藏的小磁铁位于小球的左上方某一位置C (图中θ=37°)时,金属小球偏离竖直方向的夹角也是37°,如图所示.已知小球的质量为m=4.8kg,该同学(含磁铁)的质量为M=50kg,(sin37°=0.6,cos37°=0.8,g=10m/s2)求此时:
(1)悬挂小球的细线的拉力大小为多少?
(2)该同学受到地面的支持力和摩擦力大小各为多少?
如右图所示, 两木块A、B的质量分别为m1和m2,两轻质弹簧K1、K2的劲度系数分别为k1和k2。A压在弹簧K1上(但不拴接),整个系统处于平衡状态。现缓慢上提A木块,直到它刚离开K1,在这过程中A、B木块移动的距离各为多少?
如图所示,半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通,一小球以一定的速度先滑上甲轨道,通过动摩擦因数为μ的CD段,又滑上乙轨道,最后离开两圆轨道。若小球在两圆轨道的最高点对轨道压力都恰好为零,试求水平CD段的长度。
如图,把一个质量为m的小球用细线悬挂起来,就成为一个摆,细线长为L(小球的半径忽略),最大偏角为θ,忽略空气阻力,重力加速度为g,求小球运动到最低点O时细线对小球的拉力。