如图所示，质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连，弹簧的劲度系数为k，一条不可伸长的轻绳绕过定滑轮，一端连物体A，另一端连一质量为m的物体C，物体A、B、C都处于静止状态．已知重力加速度为g，忽略一切摩擦．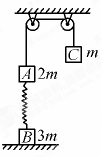
(1)求物体B对地面的压力；
(2)把物体C的质量改为5m，这时C缓慢下降，经过一段时间系统达到新的平衡状态，这时B仍没离开地面，且C只受重力和绳的拉力作用，求此过程中物体A上升的高度．
相关试题
如下图所示，一根轻质细杆的O点是一光滑水平轴，在杆的A点和B点各固定一个小球，已知AO="l" ，AB=2l，小球的质量mA＝mB＝m。将细杆从水平位置由静止开始释放，求当B球转到O点正下方时，O点受到细杆的拉力大小? 
在真空中存在空间范围足够大的、水平向右的匀强电场。若将一个质量为m、带正电电量q的小球在此电场中由静止释放，小球将沿与竖直方向夹角为
的直线运动。现将该小球从电场中某点以初速度v0竖直向上抛出，求运动过程中（取sin37°=0.6，cos37°=0.8）小球受到的电场力的大小及方向；
小球运动的抛出点至最高点之间的电势差U．
如图所示，正方形ABCD处在一个匀强电场中，电场线与正方形所在平面平行。已知A、B、C三点的电势依次为UA=6.0V，UB=4.0V，UC=-2.0V．
求D点的电势UD．
在图中画出过A点的电场线（要把作图过程画在图上，只画最后结果不能得分）。
一辆汽车在平直公路上做匀变速直线运动，公路边每隔15m有一棵树，如图所示，汽车通过AB两相邻的树用了3s，通过BC两相邻的树用了2s，求汽车运动的加速度和通过树B时的速度为多少?
粤公网安备 44130202000953号