已知 是球
是球 表面上的点,
表面上的点,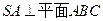 ,
, ,
,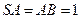 ,
, ,则球
,则球 的表面积等于 ( )
的表面积等于 ( )
A.4 |
B.3 |
C.2 |
D. |
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高
的最小值为 ( )
A.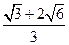 |
B.2+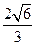 |
C.4+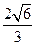 |
D.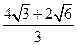 |
(本小题满分12分)经过长期观测得到:在交通繁忙的时段内,某 公路段汽车
公路段汽车
的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为:
 .
.
(1)在该时段内,当汽车的平均速度 为多少时,车流量最大?最大车流量为多少?(保留分数形式)
为多少时,车流量最大?最大车流量为多少?(保留分数形式)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
用“二分法”求方程 在区间
在区间 内的实根,取区间中点为
内的实根,取区间中点为 ,那么下一个有根的区间是 。
,那么下一个有根的区间是 。
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则
m的范围是( )
| A.(1,2) | B.(2, +∞) +∞) |
C.[3,+∞ |
D.(3,+∞) |
如图,在半径为r 的圆内作内接正六边形,再 作正六边形的内切圆,又在此内切
作正六边形的内切圆,又在此内切
圆内作内接正六边形,如此无限继续下去,设 为前n个圆的面积之和,则
为前n个圆的面积之和,则
 =( )
=( )
A.2 |
B.  |
C.4 |
D.6 |
已知等比数列{ }中,各项都是正数,且
}中,各项都是正数,且 ,
, 成等差数列,则
成等差数列,则
( )
A. |
B. |
C. |
D. |
一给定函数 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意 ,由关系式
,由关系式 得到的数列
得到的数列 满足
满足 ,则该函数的图象是( )
,则该函数的图象是( )
若数列 满足:对任意的
满足:对任意的 ,只有有限个正整数
,只有有限个正整数 使得
使得 成立,记
成立,记
这样的 的个数为
的个数为 ,则得到一个新数列
,则得到一个新数列 .例如,若数列
.例如,若数列 是
是 ,
,
则数列 是
是 .已知对任意的
.已知对任意的 ,
, ,则
,则 ,
,
 .
.
已知︱ ︱=1,︱
︱=1,︱ ︱=
︱= ,
, =0,点C在∠AOB内,且∠AOC=30°,
=0,点C在∠AOB内,且∠AOC=30°,
设 =m
=m +n
+n (m、n∈R),则
(m、n∈R),则 等于 ( )
等于 ( )
A. |
B.3 | C. |
D. |
(理)已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂
直于ABCD所在的平面,且GC=2,点B到平面EFG的距离为 ( )
A. B.
B. C.
C. D.
D.
(文)已知 和点M满足
和点M满足 .若存在实数m使得
.若存在实数m使得 成立,则m=" " ( )
成立,则m=" " ( )
| A.2 | B.3 | C.4 | D.5 |
(文)设过点 的直线分别与
的直线分别与 轴的正半轴和
轴的正半轴和 轴的正半轴交于
轴的正半轴交于 两点,点
两点,点 与点
与点 关于
关于 轴对称,
轴对称, 为坐标原点,若
为坐标原点,若 且
且 ,则点
,则点 的轨迹方程是 ( )
的轨迹方程是 ( )
A. |
B. |
C. |
D. |