2012届新人教版高三上学期单元测试(3)数学试卷
一条直线与一个平面所成的角等于 ,另一直线与这个平面所成的角是
,另一直线与这个平面所成的角是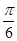 。则这
。则这
两条直线的位置关系 ( )
| A.必定相交 | B.平行 | C.必定异面 | D.不可能平行 |
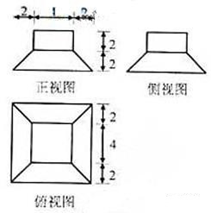
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
A.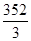 cm3 cm3 |
B.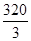 cm3 cm3 |
C.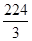 cm3 cm3 |
D. cm3 cm3 |
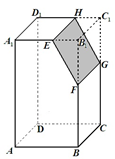
如图,若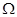 是长方体
是长方体 被平面
被平面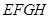 截去几何体
截去几何体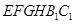 后
后
得到的几何体,其中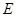 为线段
为线段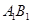 上异于
上异于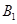 的点,
的点,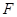 为线段
为线段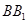 上异于
上异于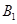 的点,且
的点,且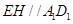 ,则下列结论中不正确的是 ( )
,则下列结论中不正确的是 ( )
A. |
B.四边形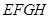 是矩形 是矩形 |
C.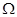 是棱柱 是棱柱 |
D.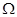 是棱台 是棱台 |
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
设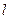 ,
,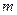 是两条不同的直线,
是两条不同的直线,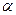 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若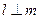 , ,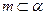 ,则 ,则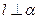 |
B.若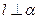 , ,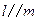 ,则 ,则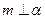 |
C.若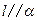 , ,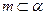 ,则 ,则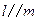 |
D.若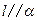 , ,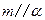 ,则 ,则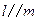 |
与正方体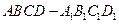 的三条棱
的三条棱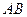 、
、 、
、 所在直线的距离相等的
所在直线的距离相等的
点 ( )
| A.有且只有1个 | B.有且只有2个 |
| C.有且只有3个 | D.有无数个 |
已知三棱锥 中,底面
中,底面 为边长等于2的等边三角形,
为边长等于2的等边三角形,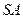 垂直于底
垂直于底
面 ,
,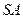 =3,那么直线
=3,那么直线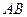 与平面
与平面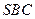 所成角的正弦值为( )
所成角的正弦值为( )
A. |
B.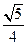 |
C. |
D.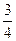 |
有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处
相连能够焊接成一个三棱锥形的铁架,则a的取值范围是 ( )
A.(0,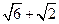 ) ) |
B.(1,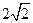 ) ) |
C.(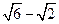 , ,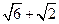 ) ) |
D.(0,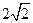 ) ) |
在半径为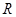 的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆
的球内有一内接正三棱锥,它的底面三个顶点恰好都在同一个大圆
上,一个动点从三棱锥的一个顶点出发沿球面运动,经过其余三点后返回,则经过的最短路
程是 ( )
A.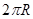 B.
B. C.
C.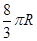 D.
D.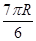
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高
的最小值为 ( )
A.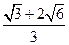 |
B.2+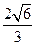 |
C.4+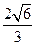 |
D.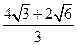 |
某地球仪上北纬 纬线的长度为
纬线的长度为 ,该地球仪的半径是__________cm,
,该地球仪的半径是__________cm,
表面积是______________cm2。
如图,矩形ABCD中,DC= ,AD=1,在DC上截取DE=1,将△ADE沿AE
,AD=1,在DC上截取DE=1,将△ADE沿AE
翻折到D1点,点D1在平面ABC上的射影落在AC上时,二面角D1—AE—B的平面角的余
弦值是 。
如图,在三棱锥 中,三条棱
中,三条棱 ,
, ,
, 两两垂直,且
两两垂直,且 >
> >
> ,
,
分别经过三条棱 ,
, ,
, 作一个截面平分三棱锥的体积,截面面积依次为
作一个截面平分三棱锥的体积,截面面积依次为 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系为 。
的大小关系为 。
如图,在透明材料制成的长方体容器ABCD—A1B1C1D1内灌注一些水,固定容
器底面一边BC于桌面上,再将容器倾斜根据倾斜度的不同,有下列命题:

(1)水的部分始终呈棱柱形;
(2)水面四边形EFGH的面积不会改变;
(3)棱A1D1始终与水面EFGH平行;
(4)当容器倾斜如图所示时,BE·BF是定值。
其中所有正确命题的序号是 。
在平面α内有△ABC,在平面α外有点S,斜线SA⊥AC,SB⊥BC,且
斜线SA、SB与平面α所成角相等。
(1)求证:AC=BC
(2)又设点S到α的距离为4cm,AC⊥BC且AB=6cm,求S与AB的距离。
平面EFGH分别平行空间四边形ABCD中的CD与AB且交BD、AD、
AC、BC于E、F、G、H.CD=a,AB=b,CD⊥AB.
(1)求证EFGH为矩形;
(2)点E在什么位置,SEFGH最大?
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,
总计耗用9.6米铁丝,再用 平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
(Ⅰ)当圆柱底面半径 取何
取何 值时,
值时, 取得最大值?并求出该最大值(结果精确到0.01平方米);
取得最大值?并求出该最大值(结果精确到0.01平方米);
(Ⅱ)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出用于灯笼的三视图(作图时,不需考虑骨架等因素)。
如图,四边形ABCD是矩形,PA⊥平面ABCD,其中AB=3,PA=4,
若在线段PD上存在点E 使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
使得BE⊥CE,求线段AD的取值范围,并求当线段PD上有且只
有一个点E使得BE⊥CE时,二面角E—BC—A正切值的大小。

如图,四棱锥P—ABCD的底面是A B=2,BC=
B=2,BC=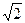 的矩形,侧面PAB
的矩形,侧面PAB
是等边三角形,且侧面PAB⊥底面ABCD
(I)证明:侧面PAB⊥侧面PBC;
(II)求侧棱PC与底面ABCD所成的角;
(III)求直线AB与平面PCD的距离.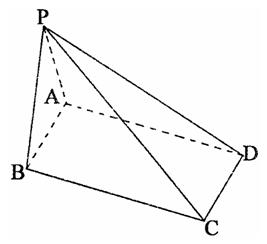
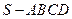 中,
中,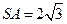 ,那么当该棱锥的体积最大时,它的高
,那么当该棱锥的体积最大时,它的高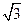
 是球
是球 表面上的点,
表面上的点,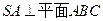 ,
, ,
,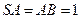 ,
, ,则球
,则球
 内有一个三棱柱
内有一个三棱柱 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱 是圆
是圆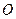 的直径。
的直径。 平面
平面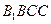 ;
;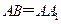 ,在圆
,在圆 柱
柱 。
。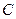 在圆周上运动时,求
在圆周上运动时,求 与平面
与平面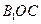 所成的角为
所成的角为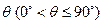 。当
。当
 的值。
的值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号