某公司准备推出一个新产品,打算拨出款项3万6
千元在本地的电视台做广告,.当地电视台广告部安排该公司的广告在晚上八点前和九点后
做广告。晚八点前的广告每秒400元,九点后的广告每秒600元,每次播出的时间在10到
60秒之间。
根据市场调查研究表明,受广告影响的人数依赖于广告播出的时间以及年龄层次,受广告影响的人数总是和广告播出的时间成正比例。广告时每秒影响各年龄组的人数(千人)估计如表所示。
现在的要求是广告宣传至少要影响1 500 000个年轻人,2 000 000个中年人和2 000 000个老年人。该公司也估计了在第一个月内受广告影响的人中,每10个年轻人中有1人、20个中年人中1人、50个老年人中1人将购买一件新产品〈并且假设没有一个人第二次再买〉,则若使第一个月的销售额最大,如何来安排广告?
某渔业公司今年初用98万元购进一艘渔船用于捕捞,第一 年需各种费用12万
年需各种费用12万
元,从第二年开始包括维修费在内,每年所需费用均比上一年增加4万元,该船每年捕捞的
总收入为50万元.
(1)该船捕捞几年开始盈利(即总收入减去成本及所有费用之差为正值)?
(2)该船捕捞若干年后,处理方案有两种:
①当年平均盈利达到最大值时,以26万元的价格卖出;
②当盈利总额达到最大值时,以8万元的价格卖出.问哪一种方案较为合算,请说明理由.
若互不相等的实数 、
、 、
、 成等差数列,
成等差数列, 、
、 、
、 成等比数列,且
成等比数列,且 ,
,
则 =( )
=( )
| A.4 | B.2 | C.-2 | D.-4 |
已知数列 、
、 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为 、
、 ,且
,且 ,
, .设
.设 (
( ),则数列
),则数列 的前10项和等于( )
的前10项和等于( )
| A.55 | B.70 | C.85 | D.100 |
数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an= .
已知a、b、c成等比数列,如果a、x、b和b、y、c都成等差数列,则 =_________.
=_________.
设 ,对于函数
,对于函数 ,下列结论正确的是 ( )
,下列结论正确的是 ( )
| A.有最大值而无最小值 | B.有最小值而无最大值 |
| C.有最大值且有最小值 | D.既无最大值又无最小值 |
已知函数 在区间
在区间 上的
上的 最小值是
最小值是
 ,则
,则 的最小值等
的最小值等
于( )
A. |
B. |
C.2 | D.3 |
在 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若
 ,则
,则
是( )
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰角三角形 |
已知函数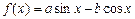 (
(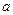 、
、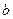 为常数,
为常数,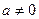 ,
,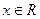 )在
)在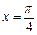 处取
处取
得最小值,则函数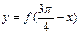 是 ( )
是 ( )
A.偶函数且它的图象关于点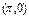 对称 对称 |
B.偶函数且它的图象关于点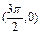 对称 对称 |
C.奇函数且它的图象关于点 对称 对称 |
D.奇函数且它的图象关于点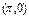 对称 对称 |
已知函数 (其中
(其中
 )
)
(1)求函数 的值域;
的值域;
(2)若函数 的图象与直线
的图象与直线 的两个相邻交点间的距离为
的两个相邻交点间的距离为 ,求函数
,求函数 的单调增区间.
的单调增区间.
已知A(-4,-5)、B(6,-1),则以线段AB为直径的圆的方程是( )
| A.(x+1)2+(y-3)2="29" | B.(x-1)2+(y+3)2="29" |
| C.(x+1)2+(y-3)2="116" | D.(x-1)2+(y+3)2=116 |