我们称满足下面条件的函数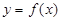 为“
为“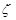 函数”:存在一条与函数
函数”:存在一条与函数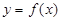 的图象有两个不同交点(设为
的图象有两个不同交点(设为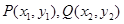 )的直线,
)的直线, 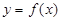 在
在 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①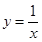 ②
②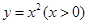 ③
③ ④
④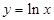 ,
,
其中为“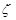 函数”的是 (将所有你认为正确的序号填在横线上)
函数”的是 (将所有你认为正确的序号填在横线上)
我们称满足下面条件的函数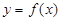 为“
为“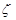 函数”:存在一条与函数
函数”:存在一条与函数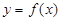 的图象有两个不同交点(设为
的图象有两个不同交点(设为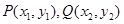 )的直线,
)的直线, 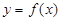 在
在 处的切线与此直线平行.下列函数:
处的切线与此直线平行.下列函数:
①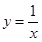 ②
②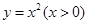 ③
③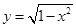 ④
④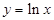 ,
,
其中为“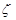 函数”的是 (将所有你认为正确的序号填在横线上)
函数”的是 (将所有你认为正确的序号填在横线上)
用数学归纳法证明不等式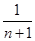 +
+ +…+
+…+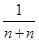 >
>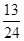 的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
的过程中,由n=k推导n=k+1时,不等式的左边增加的式子是________.
已知f1(x)=sin x+cos x,记f2(x)=f1′(x),f3(x)=f2′(x),…,fn(x)=fn-1′(x)(n∈N*,n≥2),则f1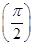 +f2
+f2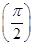 +…+f2 014
+…+f2 014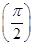 =________.
=________.
在棱长为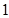 的正方体
的正方体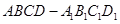 中,点
中,点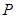 是正方体棱上一点(不包括棱的端点),
是正方体棱上一点(不包括棱的端点),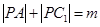 ,
,
①若 ,则满足条件的点
,则满足条件的点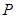 的个数为________;
的个数为________;
②若满足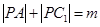 的点
的点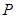 的个数为
的个数为 ,则
,则 的取值范围是________.
的取值范围是________.
已知函数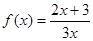 , 数列
, 数列 满足
满足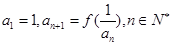 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,若
,若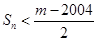 对一切
对一切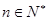 成立,求最小正整数m.
成立,求最小正整数m.
设 分别为椭圆
分别为椭圆 :
: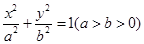 的左右顶点,
的左右顶点, 为右焦点,
为右焦点, 为
为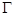 在点
在点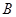 处的切线,
处的切线,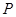 为
为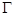 上异于
上异于 的一点,直线
的一点,直线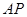 交
交 于
于 ,
,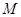 为
为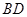 中点,有如下结论:①
中点,有如下结论:①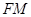 平分
平分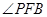 ;②
;②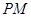 与椭圆
与椭圆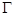 相切;③
相切;③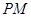 平分
平分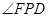 ;④使得
;④使得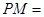
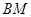 的点
的点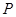 不存在.其中正确结论的序号是_____________.
不存在.其中正确结论的序号是_____________.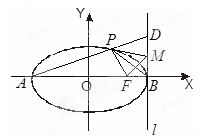
如图,△OAB是边长为2的正三角形,记△OAB位于直线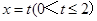 左侧的图形的面积为
左侧的图形的面积为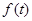 ,则
,则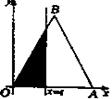
(1)函数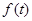 的解析式为_______;
的解析式为_______;
(2)函数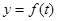 的图像在点P(t0,f(t0))处的切线的斜率为
的图像在点P(t0,f(t0))处的切线的斜率为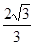 ,则t0=____________.
,则t0=____________.
在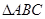 中,不等式
中,不等式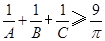 成立;在凸四边形ABCD中,
成立;在凸四边形ABCD中,
不等式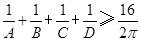 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式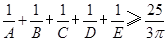 成立,,依此类推,在凸n边形
成立,,依此类推,在凸n边形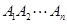 中,不等式
中,不等式 __ ___成立.
__ ___成立.
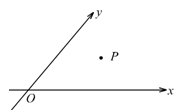
如图,设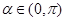 ,且
,且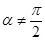 .当
.当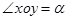 时,定义平面坐标系
时,定义平面坐标系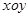 为
为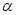 -仿射坐标系,在
-仿射坐标系,在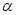 -仿射坐标系中,任意一点
-仿射坐标系中,任意一点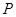 的斜坐标这样定义:
的斜坐标这样定义: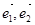 分别为与
分别为与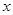 轴、
轴、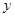 轴正向相同的单位向量,若
轴正向相同的单位向量,若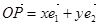 ,则记为
,则记为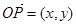 ,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
,那么在以下的结论中,正确的有.(填上所有正确结论的序号)
①设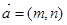 、
、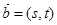 ,若
,若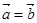 ,则
,则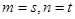 ;
;
②设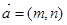 ,则
,则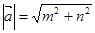 ;
;
③设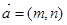 、
、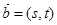 ,若
,若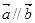 ,则
,则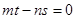 ;
;
④设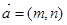 、
、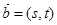 ,若
,若 ,则
,则 ;
;
⑤设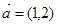 、
、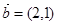 ,若
,若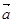 与
与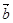 的夹角
的夹角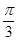 ,则
,则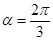 .
.
某种产品按下列三种方案两次提价.方案甲:第一次提价p%,第二次提价q%;方案乙:第一次提价q%,第二次提价p%;方案丙:第一次提价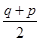 %,第二次提价
%,第二次提价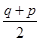 %.其中p>q>0,上述三种方案中提价最多的是________.
%.其中p>q>0,上述三种方案中提价最多的是________.
过点M(2,-2p)作抛物线x2=2py(p>0)的两条切线,切点分别为A,B,若线段AB的中点的纵坐标为6,则p的值是________.
设函数f(x),g(x)的定义域分别为M,N,且M是N真子集,若对任意的x∈M,都有g(x)=f(x),则称g(x)是f(x)的“拓展函数”.已知函数f(x)=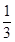 log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.
log2x,若g(x)是f(x)的“拓展函数”,且g(x)是偶函数,则符合条件的一个g(x)的解析式是________.
双曲线 =1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是________.
=1(a>0,b>0)的两条渐近线将平面划分为“上、下、左、右”四个区域(不含边界),若点(1,2)在“上”区域内,则双曲线离心率e的取值范围是________.
如图是见证魔术师“论证”64=65飞神奇.对这个乍看起来颇为神秘的现象,我们运用数学知识不难发现其中的谬误.另外,我们可以更换图中的数据,就能构造出许多更加直观与“令人信服”的“论证”.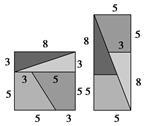
请你用数列知识归纳:(1)这些图中的数所构成的数列:________;(2)写出与这个魔术关联的一个数列递推关系式:________.