设函数f(x)=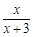 (x>0),观察:f1(x)=f(x)=
(x>0),观察:f1(x)=f(x)=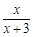 , f2(x)=f(f1(x))=
, f2(x)=f(f1(x))= , f3(x)=f(f2(x))=
, f3(x)=f(f2(x))=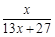 , f4(x)=f(f3(x))=
, f4(x)=f(f3(x))=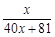 ……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
……根据以上事实,由归纳推理可得:当n∈N*, n≥2时,fn(x)=f(n-1(x))= .
已知函数 是定义域为
是定义域为 的偶函数,当
的偶函数,当 时,
时, 若关于
若关于 的方程
的方程 有且仅有
有且仅有 个不同实数根,则实数
个不同实数根,则实数 的取值范围是
的取值范围是
如图,直线 平面
平面 ,垂足为
,垂足为 ,直线
,直线 是平面
是平面 的一条斜线,斜足为
的一条斜线,斜足为 ,其中
,其中 ,过点
,过点 的动直线
的动直线 交平面
交平面 于点
于点 ,
, ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①若 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;
②若 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;
③若 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;
④ ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;
⑤ ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.
【改编】在棱长为 的正方体
的正方体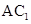 中,点
中,点 为侧面
为侧面 内一动点(不含边界),若动点
内一动点(不含边界),若动点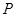 始终满足
始终满足 ,则动点
,则动点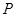 的轨迹为________.
的轨迹为________.
【改编】已知 和
和 是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在
是平面内互相垂直的两条直线,它们的交点为A,异于点A的两动点B、C分别在 、
、 上,且BC=
上,且BC= ,BC中点为M,则点M的轨迹的面积为 .
,BC中点为M,则点M的轨迹的面积为 .
已知函数 满足
满足 ,且
,且 是偶函数,当
是偶函数,当 时,
时, ,若在区间
,若在区间 内,函数
内,函数 有
有 个零点,则实数
个零点,则实数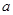 的取值范围是 .
的取值范围是 .
在平面直角坐标系 中,圆
中,圆 :
: ,圆
,圆 :
: .若圆
.若圆 上存在一点
上存在一点 ,使得过点
,使得过点 可作一条射线与圆
可作一条射线与圆 依次交于点
依次交于点 ,
, ,满足
,满足 ,则半径r的取值范围是 .
,则半径r的取值范围是 .
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y= 的图象如图所示,
的图象如图所示,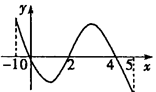
| x |
-1 |
0 |
4 |
5 |
| f(x) |
1 |
2 |
2 |
1 |
下列关于f(x)的命题:
①函数f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值是4;
④当1<a<2时,函数y=f(x)-a有4个零点;
⑤函数y=f(x)-a的零点个数可能为0,1,2,3,4.
其中正确命题的序号是___________________(写出所有正确命题的序号).
已知数列{ }通项公式为
}通项公式为 =-n+p,数列{
=-n+p,数列{ }通项公式为
}通项公式为 =
= ,设
,设 =
= 若在数列{
若在数列{ }中,
}中, >
> (n∈N﹡,n≠8),则实数p的取值范围是_______.
(n∈N﹡,n≠8),则实数p的取值范围是_______.
如图,四边形 是边长为1的正方形,点D在OA的延长线上,且
是边长为1的正方形,点D在OA的延长线上,且 ,点
,点 为
为 内(含边界)的动点,设
内(含边界)的动点,设 ,则
,则 的最大值等于 .
的最大值等于 .
【原创】设 是定义在
是定义在 上的函数,且对任意
上的函数,且对任意 ,均有
,均有 成立,若函数
成立,若函数 有最大值
有最大值 和最小值
和最小值 ,则
,则 =__________.
=__________.
对于 个互异的实数,可以排成
个互异的实数,可以排成 行
行 列的矩形数阵,如图所示的
列的矩形数阵,如图所示的 行
行 列的矩形数阵就是其中之一.将
列的矩形数阵就是其中之一.将 个互异的实数排成
个互异的实数排成 行
行 列的矩形数阵后,把每行中最大的数选出,记为
列的矩形数阵后,把每行中最大的数选出,记为 ,并设其中最小的数为
,并设其中最小的数为 ;把每列中最小的数选出,记为
;把每列中最小的数选出,记为 ,并设其中最大的数为
,并设其中最大的数为 .
.

两位同学通过各自的探究,分别得出两个结论如下:
① 和
和 必相等; ②
必相等; ② 和
和 可能相等;
可能相等;
③ 可能大于
可能大于 ; ④
; ④ 可能大于
可能大于 .
.
以上四个结论中,正确结论的序号是__________________(请写出所有正确结论的序号).