(本小题满分12分)如图所示,直三棱柱 的各条棱长均为
的各条棱长均为 ,
, 是侧棱
是侧棱 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求平面 与平面
与平面 所成二面角(锐角)的大小.
所成二面角(锐角)的大小.
(本小题满分12分)2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿。某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组: ,
,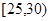 ,
,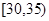 ,
, ,
, ,根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。
,根据调查结果得出年龄情况残缺的频率分布直方图如下图所示。
(1)根据已知条件,补充画完整频率分布直方图,并估计该电影院观看此部电影的观众年龄的平均数;
(2)现在从年龄属于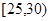 和
和 的两组中随机抽取2人,求他们属于同一年龄组的概率。
的两组中随机抽取2人,求他们属于同一年龄组的概率。
已知椭圆 的离心率为
的离心率为 ,且它的一个焦点
,且它的一个焦点 的坐标为
的坐标为 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设过焦点 的直线与椭圆相交于
的直线与椭圆相交于 两点,
两点, 是椭圆上不同于
是椭圆上不同于 的动点,试求
的动点,试求 的面积的最大值.
的面积的最大值.
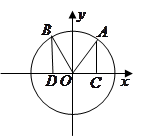
(本小题满分13分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上,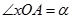 ,且
,且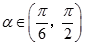 .
.
(1)若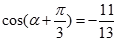 ,求
,求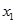 的值;
的值;
(2)若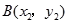 也是单位圆
也是单位圆 上的点,且
上的点,且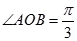 .过点
.过点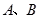 分别做
分别做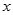 轴的垂线,垂足为
轴的垂线,垂足为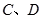 ,记
,记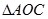 的面积为
的面积为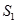 ,
, 的面积为
的面积为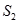 .设
.设 ,求函数
,求函数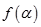 的最大值.
的最大值.
(本小题12分)已知 的两边
的两边 的长是关于
的长是关于 的一元二次方程
的一元二次方程 的两个实数根,第三边BC长为5.
的两个实数根,第三边BC长为5.
(1) 为何值时,
为何值时, 是以
是以 为斜边的直角三角形。
为斜边的直角三角形。
(2) 为何值时,
为何值时, 是等腰三角形,并求此时三角形的周长。
是等腰三角形,并求此时三角形的周长。
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 处的切线方程;
处的切线方程;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)若函数 有两个极值点
有两个极值点 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知数列 中,
中, ,
, ,2,3,…
,2,3,…
(Ⅰ)求证数列 是等差数列;
是等差数列;
(Ⅱ)试比较 的大小;
的大小;
(Ⅲ)求正整数 ,使得对于任意的正整数
,使得对于任意的正整数 恒成立.
恒成立.
(本小题满分12分)在平面直角坐标系 中,已知圆心在
中,已知圆心在 轴上,半径为4的圆
轴上,半径为4的圆 位于
位于 轴右侧,且与
轴右侧,且与 轴相切.
轴相切.
(I)求圆 的方程;
的方程;
(II)若椭圆 的离心率为
的离心率为 ,且左右焦点为
,且左右焦点为 .试探究在圆
.试探究在圆 上是否存在点
上是否存在点 ,使得
,使得 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
(本小题满分12分)已知椭圆C: 过点
过点
 ,离心率为
,离心率为 ,点
,点 分别为其左右焦点.
分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点 ,且
,且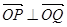 ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
已知函数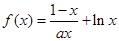 在(1,+∞)上是增函数,且a>0.
在(1,+∞)上是增函数,且a>0.
(1)求a的取值范围;
(2)求函数 在[0,+∞)上的最大值;
在[0,+∞)上的最大值;
(3)设a>1,b>0,求证: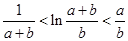 .
.
(本小题满分14分)已知椭圆: 的一个焦点为
的一个焦点为 ,且过点
,且过点 ,右顶点为
,右顶点为 ,经过点
,经过点 的动直线
的动直线 与椭圆交于
与椭圆交于 两点.
两点.
(1)求椭圆方程;
(2)记 和
和 的面积分别为
的面积分别为 ,求
,求 的最大值;
的最大值;
(3)在 轴上是否存在一点
轴上是否存在一点 ,使得点
,使得点 关于
关于 轴的对称点落在直线
轴的对称点落在直线 上?若存在,则
上?若存在,则
求出 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
(本小题共13分)已知椭圆 的离心率为
的离心率为 ,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为
,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为 的直线
的直线 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于 ,
, 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围;
的取值范围;
(Ⅲ)试用 表示△
表示△ 的面积,并求面积的最大值.
的面积,并求面积的最大值.