已知数列 的前
的前 项和为
项和为 ,
, ,且
,且 (
( 为正整数)
为正整数)
(1)求数列 的通项公式;
的通项公式;
(2)对任意正整数 ,是否存在
,是否存在 ,使得
,使得 恒成立?若存在,求是实数
恒成立?若存在,求是实数 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
在平面直角坐标系中,已知椭圆
.如图所示,斜率为
且不过原点的直线
交椭圆
于
,
两点,线段
的中点为
,射线
交椭圆
于点
,交直线
于点
.
(1)求的最小值;
(2)若
(i)求证:直线过定点;
(ii)试问点能否关于
轴对称?若能,求出此时
的外接圆方程;若不能,请说明理由.

设函数
(1)若为
的极值点,求实数
;
(2)求实数的取值范围,使得对任意的
,恒有
成立.注:e为自然对数的底数.
(1)已知函数,求函数
的最大值;
(2)设均为正数,证明:
①若,则
;
②若,则
已知双曲线C: 离心率是
离心率是 ,过点
,过点 ,且右支上的弦
,且右支上的弦 过右焦点
过右焦点 .
.
(1)求双曲线C的方程;
(2)求弦 的中点
的中点 的轨迹E的方程;
的轨迹E的方程;
(3)是否存在以 为直径的圆过原点O?,若存在,求出直线
为直径的圆过原点O?,若存在,求出直线 的斜率k 的值.若不存在,则说明理由.
的斜率k 的值.若不存在,则说明理由.
已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 <
< 时,求实数
时,求实数 取值范围.
取值范围.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(1)证明:BD⊥AA1;
(2)求锐二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
设函数 .
.
(1)若曲线 在点
在点 处与直线
处与直线 相切,求a,b的值;
相切,求a,b的值;
(2)求函数 的单调区间.
的单调区间.
如图,已知双曲线C1: -y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
-y2=1,曲线C2:|y|=|x|+1.P是平面内一点.若存在过点P的直线与C1,C2都有共同点,则称P为“C1-C2型点”.
(1)在正确证明C1的左焦点是“C1-C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证).
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1-C2型点”.
(3)求证:圆x2+y2= 内的点都不是“C1-C2型点”.
内的点都不是“C1-C2型点”.
已知点P是圆M:x2+(y+m)2=8(m>0,m≠ )上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
)上一动点,点N(0,m)是圆M所在平面内一定点,线段NP的垂直平分线l与直线MP相交于点Q.
(1)当P在圆M上运动时,记动点Q的轨迹为曲线Г,判断曲线Г为何种曲线,并求出它的标准方程.
(2)过原点斜率为k的直线交曲线Г于A,B两点,其中A在第一象限,且它在x轴上的射影为点C,直线BC交曲线Г于另一点D,记直线AD的斜率为k′,是否存在m,使得对任意的k>0,都有|k·k′|=1?若存在,求m的值;若不存在,请说明理由.
已知☉M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切☉M于A,B两点.
(1)如果|AB|= ,求直线MQ的方程.
,求直线MQ的方程.
(2)求证:直线AB恒过一个定点.
在直角坐标平面上给定一曲线y2=2x,
(1)设点A的坐标为 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.
一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.
(1)求证:AC⊥BD.
(2)求三棱锥E-BCD的体积.
已知椭圆
 的两个焦点分别为
的两个焦点分别为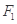 ,
,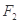 ,离心率为
,离心率为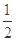 ,过
,过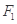 的直线
的直线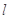 与椭圆
与椭圆 交于
交于 两点,且
两点,且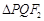 的周长为
的周长为 .
.
(I)求椭圆 的方程;
的方程;
(Ⅱ)过原点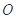 的两条互相垂直的射线与椭圆
的两条互相垂直的射线与椭圆 分别交于
分别交于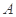 ,
,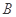 两点,求证:点
两点,求证:点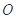 到直线
到直线 的距离为定值,并求出这个定值.
的距离为定值,并求出这个定值.
已知椭圆
 的两个焦点分别为
的两个焦点分别为 ,
, ,离心率为
,离心率为 ,过
,过 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 的周长为
的周长为 .
.
(1)求椭圆 的方程;
的方程;
(2)斜率为 的直线
的直线 与曲线
与曲线 交于
交于 两个不同点,若直线
两个不同点,若直线 不过点
不过点 ,设直线
,设直线 的斜率分别为
的斜率分别为 ,求
,求 的数值;
的数值;
(3)试问:是否存在一个定圆 ,与以动点
,与以动点 为圆心,以
为圆心,以 为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.
为半径的圆相内切?若存在,求出这个定圆的方程;若不存在,说明理由.