在直角坐标系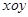 中,曲线
中,曲线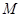 的参数方程为
的参数方程为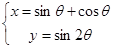
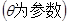 .若以该直角坐标系的原点
.若以该直角坐标系的原点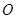 为极点,
为极点,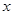 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线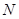 的极坐标方程为:
的极坐标方程为: (其中
(其中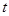 为常数)
为常数)
(1)若曲线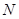 与曲线
与曲线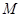 只有一个公共点,求
只有一个公共点,求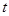 的取值范围;
的取值范围;
(2)当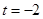 时,求曲线
时,求曲线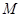 上的点与曲线
上的点与曲线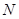 上点的最小距离
上点的最小距离
如图,已知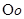 是
是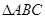 的外接圆,AB=BC,AD是BC边上的高,AE是
的外接圆,AB=BC,AD是BC边上的高,AE是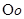 的直径.
的直径.
(1)求证: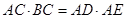 ;
;
(2)过点C作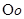 的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
的切线交BA的延长线于点F,若AF=4,CF=6,求AC的长.
已知函数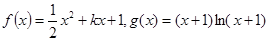
(1)若函数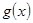 的图象在原点处的切线
的图象在原点处的切线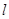 与函数
与函数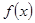 的图象相切,求实数k的值;
的图象相切,求实数k的值;
(2)若对于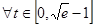 ,总存在
,总存在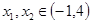 ,且
,且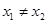 满足
满足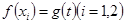 ,其中e为自然对数的底数,求实数k的取值范围.
,其中e为自然对数的底数,求实数k的取值范围.
如图,在平面直角坐标系xOy中,平行于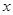 轴且过点
轴且过点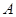 (3,2)的入射光线
(3,2)的入射光线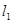 被直线
被直线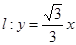 反射.反射光线
反射.反射光线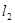 交
交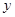 轴于
轴于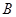 点,圆
点,圆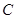 过点
过点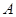 且与
且与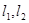 都相切.
都相切.
(1)求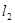 所在直线的方程和圆
所在直线的方程和圆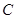 的方程;
的方程;
(2)设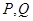 分别是直线
分别是直线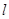 和圆
和圆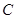 上的动点,求
上的动点,求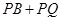 的最小值及此时点
的最小值及此时点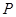 的坐标.
的坐标.
已知点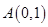 ,点
,点 在双曲线
在双曲线 上.
上.
(Ⅰ)当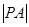 最小时,求点
最小时,求点 的坐标;
的坐标;
(Ⅱ)过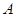 点的直线
点的直线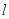 与双曲线
与双曲线 的左、右两支分别交于
的左、右两支分别交于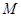 、
、 两点,
两点,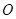 为坐标原点,若
为坐标原点,若 的面积为
的面积为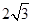 ,求直线
,求直线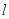 的方程.
的方程.
已知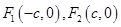 是椭圆的
是椭圆的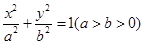 左、右焦点,过点
左、右焦点,过点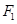 作倾斜角为
作倾斜角为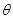 的
的
动直线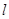 交椭圆于
交椭圆于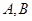 两点.当
两点.当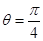 时,
时,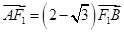 ,且
,且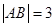 .
.
(1)求椭圆的离心率及椭圆的标准方程;
(2)求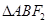 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线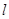 的方程.
的方程.
如图,在平面直角坐标系 中,椭圆
中,椭圆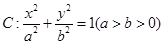 的离心率为
的离心率为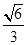 ,直线
,直线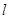 与
与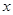 轴交于点
轴交于点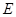 ,与椭圆
,与椭圆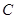 交于
交于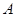 、
、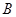 两点.当直线
两点.当直线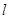 垂直于
垂直于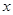 轴且点
轴且点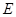 为椭圆
为椭圆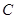 的右焦点时, 弦
的右焦点时, 弦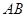 的长为
的长为 .
.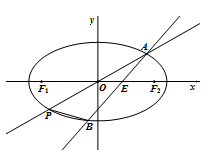
(1)求椭圆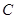 的方程;
的方程;
(2)若点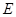 的坐标为
的坐标为 ,点
,点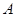 在第一象限且横坐标为
在第一象限且横坐标为 ,连结点
,连结点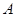 与原点
与原点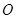 的直线交椭圆
的直线交椭圆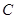 于另一点
于另一点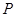 ,求
,求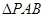 的面积;
的面积;
(3)是否存在点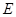 ,使得
,使得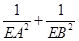 为定值?若存在,请指出点
为定值?若存在,请指出点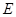 的坐标,并求出该定值;若不存在,请说明理由.
的坐标,并求出该定值;若不存在,请说明理由.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍,某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如下图所示.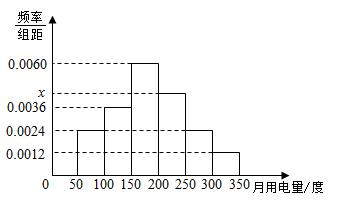
(1)为降低能源损耗,节约用电,规定:每间宿舍每月用电量不超过200度时,按每度0.5元收取费用;超过200度,超过部分按每度1元收取费用。以t表示某宿舍的用电量(单位:度),以y表示该宿舍的用电费用(单位:元),求y与t的函数关系式?
(2)求图中月用电量在(200,250]度的宿舍有多少间?
(3)在直方图中,以各组的区间中点值代表该组的各个值,宿舍用电量落入该区间的频率作为宿舍用电量取该区间中点值的频率(例如:若t∈[150,200),则取t=175,且t=175发生的频率等于落入[150,200)的频率),试估计我校学生宿舍的月均用电费用.