已知函数 .
.
(1)当 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 图像上的点都在
图像上的点都在 所表示的平面区域内,求实数
所表示的平面区域内,求实数 的取值范围.
的取值范围.
已知椭圆 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(1)求椭圆 的方程;
的方程;
(2)已知 为椭圆
为椭圆 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线 对称,并说明理由.
对称,并说明理由.
(本小题满分13分)
已知数列 ,设
,设  ,数列
,数列 .
.
(I)求证: 是等差数列;
是等差数列;
(II)求数列 的前n项和Sn;
的前n项和Sn;
(Ⅲ)若 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长为
轴上,长轴长为 ,且点
,且点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 长轴上的一个动点,过
长轴上的一个动点,过 作方向向量
作方向向量 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,求证:
两点,求证: 为定值.
为定值.
已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)若曲线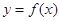 在点
在点 处的切线平行于
处的切线平行于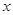 轴,求
轴,求 的值;
的值;
(2)求函数 的极值;
的极值;
(3)当 的值时,若直线
的值时,若直线 与曲线
与曲线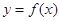 没有公共点,求
没有公共点,求 的最大值.
的最大值.
(注:可能会用到的导数公式: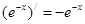 ;
; )
)
已知函数
(1)当 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)当 时,若
时,若 在区间
在区间 上的最小值为-2,求
上的最小值为-2,求 的取值范围;
的取值范围;
(3)若对任意 ,且
,且 恒成立,求
恒成立,求 的取值.
的取值.
已知函数 在
在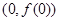 处切线为
处切线为 .
.
(1)求 的解析式;
的解析式;
(2)设 ,
, ,
, ,
, 表示直线
表示直线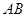 的斜率,求证:
的斜率,求证: .
.
如图,已知点 是离心率为
是离心率为 的椭圆
的椭圆 :
:
 上的一点,斜率为
上的一点,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 ,
, 两点,且
两点,且 、
、 、
、 三点互不重合.
三点互不重合.
(1)求椭圆 的方程;(2)求证:直线
的方程;(2)求证:直线 ,
, 的斜率之和为定值.
的斜率之和为定值.
已知椭圆 的右焦点为
的右焦点为 ,点
,点 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)点 在圆
在圆 上,且
上,且 在第一象限,过
在第一象限,过 作圆
作圆 的切线交椭圆于
的切线交椭圆于 ,
, 两点,问:△
两点,问:△ 的周长是否为定值?如果是,求出定值;如果不是,说明理由.
的周长是否为定值?如果是,求出定值;如果不是,说明理由.
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,  为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.
如图,已知在四棱锥 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
, ,
, 是
是 的中点,
的中点, 是线段
是线段 上的点.
上的点.
(1)当 是
是 的中点时,求证:
的中点时,求证: 平面
平面 ;
;
(2)要使二面角 的大小为
的大小为 ,试确定
,试确定 点的位置.
点的位置.
设等差数列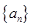 的公差为
的公差为 ,且
,且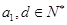 .若设
.若设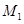 是从
是从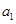 开始的前
开始的前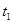 项数列的和,即
项数列的和,即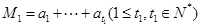 ,
,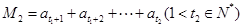 ,如此下去,其中数列
,如此下去,其中数列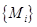 是从第
是从第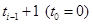 开始到第
开始到第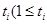 )项为止的数列的和,即
)项为止的数列的和,即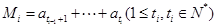 .
.
(1)若数列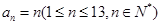 ,试找出一组满足条件的
,试找出一组满足条件的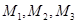 ,使得:
,使得:  ;
;
(2)试证明对于数列 ,一定可通过适当的划分,使所得的数列
,一定可通过适当的划分,使所得的数列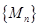 中的各数都为平方数;
中的各数都为平方数;
(3)若等差数列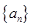 中
中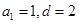 .试探索该数列中是否存在无穷整数数列
.试探索该数列中是否存在无穷整数数列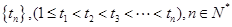 ,使得
,使得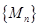 为等比数列,如存在,就求出数列
为等比数列,如存在,就求出数列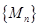 ;如不存在,则说明理由.
;如不存在,则说明理由.