已知

(1)当 时,求
时,求 的极大值点;
的极大值点;
(2)设函数 的图象
的图象 与函数
与函数 的图象
的图象 交于
交于 、
、 两点,过线段
两点,过线段 的中点做
的中点做 轴的垂线分别交
轴的垂线分别交 、
、 于点
于点 、
、 ,证明:
,证明: 在点
在点 处的切线与
处的切线与 在点
在点 处的切线不平行.
处的切线不平行.
已知椭圆C的中心在原点,一个焦点F(-2,0),且长轴长与短轴长的比为 ,
,
(1)求椭圆C的方程;
(2)设点M(m,0)在椭圆C的长轴上,设点P是椭圆上的任意一点,若当 最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
最小时,点P恰好落在椭圆的右顶点,求实数m的取值范围.
已知函数f(x)=ax2+ln(x+1).
(1)当a= 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当 时,函数y=f(x)图像上的点都在
时,函数y=f(x)图像上的点都在 所表示的平面区域内,求实数a的取值范围;
所表示的平面区域内,求实数a的取值范围;
(3)求证: (其中
(其中 ,e是自然数对数的底数)
,e是自然数对数的底数)
如图,椭圆C: 的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
(1)若点P的坐标 ,求m的值;
,求m的值;
(2)若椭圆C上存在点M,使得 ,求m的取值范围.
,求m的取值范围.
设等比数列{an}的前n项和为Sn.已知an+1=2Sn+2( )
)
(1)求数列{an}的通项公式;
(2)在an与an+1之间插入n个数,使这n+2个数组成一个公差为dn的等差数列,
①在数列{dn}中是否存在三项dm,dk,dp(其中m,k,p成等差数列)成等比数列?若存在,求出这样的三项,若不存在,说明理由;
②求证: .
.
已知椭圆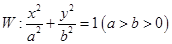 的焦距为
的焦距为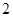 ,过右焦点和短轴一个端点的直线的斜率为
,过右焦点和短轴一个端点的直线的斜率为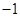 ,
,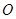 为坐标原点.
为坐标原点.
(1)求椭圆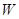 的方程.
的方程.
(2)设斜率为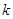 的直线
的直线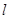 与
与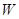 相交于
相交于 、
、 两点,记
两点,记 面积的最大值为
面积的最大值为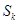 ,证明:
,证明: .
.
在数列 中,
中, .从数列
.从数列 中选出
中选出 项并按原顺序组成的新数列记为
项并按原顺序组成的新数列记为 ,并称
,并称 为数列
为数列 的
的 项子列.例如数列
项子列.例如数列 、
、 、
、 、
、 为
为 的一个
的一个 项子列.
项子列.
(1)试写出数列 的一个
的一个 项子列,并使其为等差数列;
项子列,并使其为等差数列;
(2)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等差数列,证明:
为等差数列,证明: 的公差
的公差 满足
满足 ;
;
(3)如果 为数列
为数列 的一个
的一个 项子列,且
项子列,且 为等比数列,证明:
为等比数列,证明:
 .
.
已知椭圆 :
: 的离心率为
的离心率为 ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆 的方程;
的方程;
(2)如图,设椭圆 的上、下顶点分别为
的上、下顶点分别为 ,
, 是椭圆上异于
是椭圆上异于 的任意一点,直线
的任意一点,直线 分别交
分别交 轴于点
轴于点 ,若直线
,若直线 与过点
与过点 的圆
的圆 相切,切点为
相切,切点为 .证明:线段
.证明:线段 的长为定值.
的长为定值.
设 是各项均不为零的
是各项均不为零的 (
( )项等差数列,且公差
)项等差数列,且公差 .
.
(1)若 ,且该数列前
,且该数列前 项和
项和 最大,求
最大,求 的值;
的值;
(2)若 ,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求
,且将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,求 的值;
的值;
(3)若该数列中有一项是 ,则数列
,则数列 中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
中是否存在不同三项(按原来的顺序)为等比数列?请说明理由.
已知 是椭圆E:
是椭圆E: 的两个焦点,抛物线
的两个焦点,抛物线 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y= 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
(1)求椭圆E的方程;
(2)如图,过点 的动直线
的动直线 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由.
已知圆
 ,若椭圆
,若椭圆 的右顶点为圆
的右顶点为圆 的圆心,离心率为
的圆心,离心率为 .
.
(1)求椭圆C的方程;
(2)若存在直线 ,使得直线
,使得直线 与椭圆
与椭圆 分别交于
分别交于 两点,与圆
两点,与圆 分别交于
分别交于 两点,点
两点,点 在线段
在线段 上,且
上,且 ,求圆
,求圆 的半径
的半径 的取值范围.
的取值范围.
已知椭圆 的由顶点为A,右焦点为F,直线
的由顶点为A,右焦点为F,直线 与x轴交于点B且与直线
与x轴交于点B且与直线 交于点C,点O为坐标原点,
交于点C,点O为坐标原点, ,过点F的直线
,过点F的直线 与椭圆交于不同的两点M,N.
与椭圆交于不同的两点M,N.
(1)求椭圆的方程;
(2)求 的面积的最大值.
的面积的最大值.
已知函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最大值;
上的最大值;
(2)令 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,又
,又 是
是 的导函数,若正常数
的导函数,若正常数 满足条件
满足条件 .证明:
.证明: .
.
如图,正三棱柱 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是 棱的中点,AE交
棱的中点,AE交 于点H.
于点H.
(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)求点 到平面
到平面 的距离.
的距离.
已知数列 的前
的前 项和为
项和为 ,对一切正整数
,对一切正整数 ,点
,点 都在函数
都在函数 的图像上,且过点
的图像上,且过点 的切线的斜率为
的切线的斜率为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,等差数列
,等差数列 的任一项
的任一项 ,其中
,其中 是
是 中所有元素的最小数,
中所有元素的最小数, ,求
,求 的通项公式.
的通项公式.