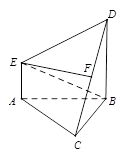
如图,在多面体 中,
中,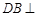 平面
平面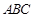 ,
,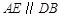 ,且
,且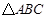 是边长为
是边长为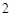 的等边三角形,
的等边三角形,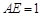 ,
,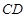 与平面
与平面 所成角的正弦值为
所成角的正弦值为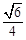 .
.
(Ⅰ)若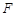 是线段
是线段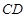 的中点,证明:
的中点,证明: 面
面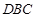 ;
;
(Ⅱ)求二面角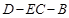 的平面角的余弦值.
的平面角的余弦值.
如图,在直三棱柱ABCA1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点.
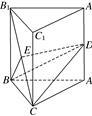
(1)求证:DE∥平面ABC;
(2)求三棱锥EBCD的体积.
某校从高三年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.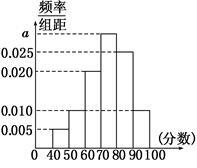
(1)求图中实数a的值;
(2)若该校高三年级共有学生640名,试估计该校高三年级期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的概率.
已知Sn是数列{an}的前n项和,且Sn=2an-2n对n∈N*成立.
(1)证明数列{an+2}是等比数列,并求出数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
已知 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 ,
, 时,有
时,有 成立.
成立.
(1)判断 在
在 上的单调性,并证明;
上的单调性,并证明;
(2)解不等式: ;
;
(3)若当 时,
时, 对所有的
对所有的 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
在平面直角坐标系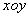 中,
中, 为坐标原点,以
为坐标原点,以 为圆心的圆与直线
为圆心的圆与直线 相切.
相切.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若直线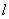 :
: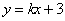 与圆
与圆 交于
交于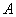 ,
, 两点,在圆
两点,在圆 上是否存在一点
上是否存在一点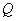 ,使得
,使得 ,若存在,求出此时直线
,若存在,求出此时直线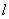 的斜率;若不存在,说明理由.
的斜率;若不存在,说明理由.
在平面直角坐标系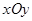 中,
中,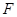 是抛物线
是抛物线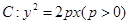 的焦点,圆
的焦点,圆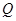 过
过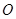 点与
点与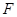 点,且圆心
点,且圆心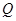 到抛物线
到抛物线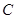 的准线的距离为
的准线的距离为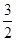 .
.
(1)求抛物线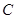 的方程;
的方程;
(2)已知抛物线上一点 ,过点
,过点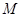 作抛物线的两条弦
作抛物线的两条弦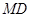 和
和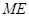 ,且
,且 ,判断直线
,判断直线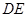 是否过定点?并说明理由.
是否过定点?并说明理由.
已知双曲线 的焦距为
的焦距为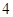 ,离心率为
,离心率为 .
.
(1)求双曲线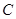 的标准方程;
的标准方程;
(2)直线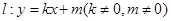 与双曲线
与双曲线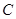 交于不同的两点
交于不同的两点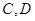 ,如果
,如果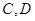 能都在以点
能都在以点 为圆心的同一个圆上,求实数
为圆心的同一个圆上,求实数 的取值范围.
的取值范围.
正项数列{an}满足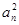 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an.
(2)令bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
如图,在平面直角坐标系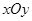 中,圆
中,圆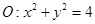 交
交 轴于点
轴于点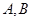 (点
(点 在
在 轴的负半轴上),点
轴的负半轴上),点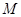 为圆
为圆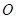 上一动点,
上一动点, 分别交直线
分别交直线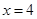 于
于 两点。
两点。
(1)求 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点 的坐标为
的坐标为 ,连接
,连接 交圆
交圆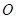 于另一点
于另一点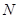 .
.
①试判断点 与以
与以 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记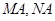 的斜率分别为
的斜率分别为 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.