已知二阶矩阵M属于特征值3的一个特征向量为 ,并且矩阵
,并且矩阵 对应的变换将点
对应的变换将点 变成点
变成点 ,求出矩阵
,求出矩阵 。
。
已知函数 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
)
(1)设 ,求证:当
,求证:当 时,
时, ;
;
(2)是否存在实数a,使得当 时,
时, 的最小值是3 ?如果存在,求出实
的最小值是3 ?如果存在,求出实
数a的值;如果不存在,请说明理
平面直角坐标系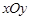 中,已知向量
中,已知向量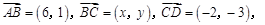 且
且 .
.
(1)求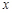 与
与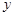 之间的关系式;
之间的关系式;
(2)若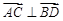 ,求四边形
,求四边形 的面积.
的面积.
已知数列 满足
满足 =-1,
=-1,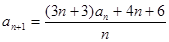 ,数列
,数列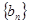 满足
满足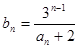
(1)求证:数列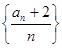 为等比数列,并求数列
为等比数列,并求数列 的通项公式.
的通项公式.
(2)求证:当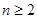 时,
时,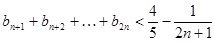
(3)设数列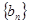 的前
的前 项和为
项和为 ,求证:当
,求证:当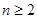 时,
时, .
.
已知圆C: 过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
过点A(3,1),且过点P(4,4)的直线PF与圆C相切并和x轴的负半轴相交于点F.
(1)求切线PF的方程;
(2)若抛物线E的焦点为F,顶点在原点,求抛物线E的方程.
(3)若Q为抛物线E上的一个动点,求 的取值范围.
的取值范围.
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求:
(Ⅰ)连续取两次都是白球的概率;
(Ⅱ)若取一个红球记2分,取一个白球记1分,取一个黑球记0 分,连续取三次分数之和为4分的概率.
已知数列 满足
满足 ,
, ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:对于一切正整数 ,有
,有 .
.
已知函数 (
( )是奇函数,
)是奇函数, 有最大值
有最大值
且 .
.
(1)求函数 的解析式;
的解析式;
(2)是否存在直线 与
与 的图象交于P、Q两点,并且使得
的图象交于P、Q两点,并且使得 、
、 两点关于点
两点关于点 对称,若存在,求出直线
对称,若存在,求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
在 中,角
中,角 所对的边分别为
所对的边分别为 ,向量
,向量  ,
, .已知
.已知  .
.
(1)若 ,求角A的大小;
,求角A的大小;
(2)若 ,求
,求 的取值范围.
的取值范围.
已知数列 是首项
是首项 的等比数列,其前
的等比数列,其前 项和
项和 中
中 ,
, ,
, 成
成
等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,若
,若 ,求证:
,求证: .
.
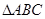 的三个内角
的三个内角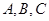 所对的边分别为
所对的边分别为 ,向量
,向量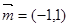 ,
,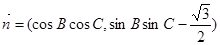 ,且
,且 .
.
(1)求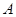 的大小;
的大小;
(2)现在给出下列三个条件:①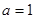 ;②
;②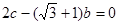 ;③
;③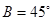 ,
,
试从中选择两个条件以确定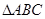 ,求出所确定的
,求出所确定的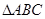 的面积.
的面积.
设不等式 确定的平面区域为
确定的平面区域为 ,
, 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取
内任取 个整点,求这些整点中恰有
个整点,求这些整点中恰有 个整点在区域
个整点在区域 内的概率;
内的概率;
(2)在区域 内任取
内任取 个点,记这
个点,记这 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望 及方差
及方差 .
.