已知圆C：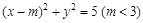
过点A（3，1），且过点P（4，4）的直线PF与圆C相切并和x轴的负半轴相交于点F．
（1）求切线PF的方程；
（2）若抛物线E的焦点为F,顶点在原点，求抛物线E的方程.
（3）若Q为抛物线E上的一个动点，求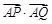
的取值范围．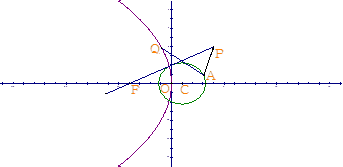
相关试题
分别为
内角A，B，C的对边，
，且
．
，求
，命题“
”为真，“
”为真，求实数
的取值范围．
，求函数
在点
处的切线方程．
．
时，求函数
的单调区间；
时，令
．求
在
上的最大值和最小值；
对
恒成立，求实数
的取值范围
上任意一点到两焦点
距离之和为
，离心率为
．
的斜率为
，直线
两点．点
为椭圆上一点，求
的面积的最大值．相关知识点
推荐套卷
已知圆C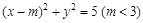：过点A（3，1），且过点P（4，4）的直线PF与圆C相切并和x轴的负半轴相交于点F．
（1）求切线PF的方程；
（2）若抛物线E的焦点为F,顶点在原点，求抛物线E的方程.
（3）若Q为抛物线E上的一个动点，求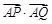的取值范围．
粤公网安备 44130202000953号