已知圆心C(1,2),且经过点(0,1)
(Ⅰ)写出圆C的标准方程;
(Ⅱ)过点P(2,﹣1)作圆C的切线,求切线的方程及切线的长.
若P(2,﹣1)为圆(x﹣1)2+y2=25的弦AB的中点,则直线AB的方程是()
| A.x﹣y﹣3=0 | B.2x+y﹣3=0 | C.x+y﹣1=0 | D.2x﹣y﹣5=0 |
已知圆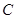 :
: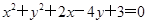 .
.
(1)若圆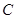 的切线在
的切线在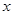 轴和
轴和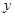 轴上的截距相等,求此切线的方程.
轴上的截距相等,求此切线的方程.
(2)从圆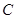 外一点
外一点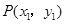 向该圆引一条切线,切点为
向该圆引一条切线,切点为 为坐标原点,且有
为坐标原点,且有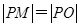 ,求使得
,求使得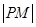 取得最小值的点
取得最小值的点 的坐标.
的坐标.
如图,在平面直角坐标系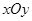 中,圆
中,圆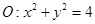 交
交 轴于点
轴于点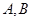 (点
(点 在
在 轴的负半轴上),点
轴的负半轴上),点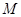 为圆
为圆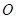 上一动点,
上一动点, 分别交直线
分别交直线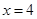 于
于 两点。
两点。
(1)求 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点 的坐标为
的坐标为 ,连接
,连接 交圆
交圆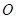 于另一点
于另一点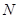 .
.
①试判断点 与以
与以 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记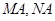 的斜率分别为
的斜率分别为 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.