设不等式 确定的平面区域为
确定的平面区域为 ,
,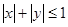 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取
内任取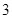 个整点,求这些整点中恰有
个整点,求这些整点中恰有 个整点在区域
个整点在区域 内的概率;
内的概率;
(2)在区域 内任取
内任取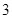 个点,记这
个点,记这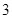 个点在区域
个点在区域 内的个数为
内的个数为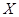 ,求
,求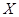 的分布列,数学期望
的分布列,数学期望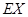 及方差
及方差 .
.
相关知识点
推荐套卷
设不等式 确定的平面区域为
确定的平面区域为 ,
,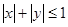 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取
内任取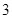 个整点,求这些整点中恰有
个整点,求这些整点中恰有 个整点在区域
个整点在区域 内的概率;
内的概率;
(2)在区域 内任取
内任取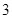 个点,记这
个点,记这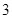 个点在区域
个点在区域 内的个数为
内的个数为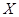 ,求
,求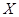 的分布列,数学期望
的分布列,数学期望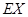 及方差
及方差 .
.